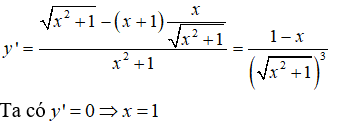GTLN của hàm số y=x+1 / căn bậc hai của x^2 +1 trên khoảng (0; 4) đạt được
Câu hỏi:
GTLN của hàm số trên khoảng (0; 4) đạt được
A. x = 1
B. x = -1
C.
D. Không tồn tại
Trả lời:
Xét
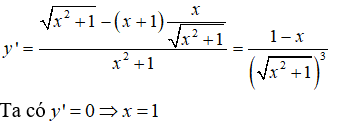
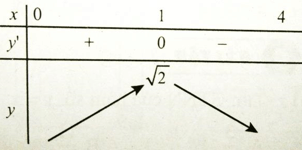
Ta có y' = 0 => x = 1
Vậy hàm số có GTLN bằng √2 khi x = 1 . Chọn đáp án A.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 2:
Giá trị lớn nhất của hàm số đạt được khi x nhận giá trị bằng
Xem lời giải »
Câu 3:
Giá trị lớn nhất của hàm số trên [0; 3] là:
Xem lời giải »
Câu 4:
Giá trị lớn nhất của hàm số có đồ thị như hình bên là
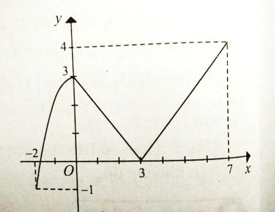
Xem lời giải »
Câu 6:
Một hành lang giữa hai tòa tháp có hình dạng một hình lăng trụ đứng. Hai mặt bên ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20m, rộng 5m. Với độ dài xấp xỉ nào của BC thì thể tích hành lang này lớn nhất
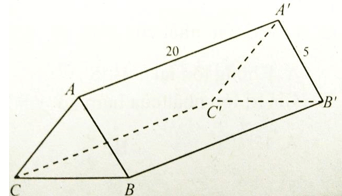
Xem lời giải »
Câu 8:
GTLN của hàm số trên đoạn [0; π] là
Xem lời giải »