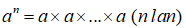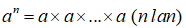Thảo luận và tìm hiểu ý tưởng thực hiện các tính toán bằng kĩ thuật đệ quy
Trao đổi, thảo luận và tìm hiểu ý tưởng thực hiện các tính toán sau bằng kĩ thuật đệ quy
Giải Chuyên đề Tin 11 Bài 2: Thiết kế thuật toán đệ quy - Kết nối tri thức
Hoạt động 1 trang 11 Chuyên đề Tin học 11: Trao đổi, thảo luận và tìm hiểu ý tưởng thực hiện các tính toán sau bằng kĩ thuật đệ quy
1. Tính tổng S(n) = 1+2+3+…+n
2. Tính lũy thừa
3. Tính n giai thừa n!= 1x2x3x…xn
Lời giải:
1. Tính tổng S(n) = 1+2+3+…+n
Bước 1. Bài toán yêu cầu tính tổng của n số nguyên từ 1 đến n. Cần thiết lập hàm S(n) trả về giá trị tổng cần tim.
Bước 2. Điều kiện n ≥ 0.
Với n = 0 ta có S(n) = 0. Đây là phần cơ sở cho điều kiện dừng của lời gọi đệ quy của hàm S(n).
Bước 3. Dễ thấy S(n) = n + S(n - 1) là công thức truy hồi của hàm S(n) và là cơ sở của lời gọi đệ quy của hàm.Chương trình như sau:
2. Tính lũy thừa
Bước 1. Bài toán yêu cầu tính luỹ thừa . Cần thiết lập hàm exp(a,n) trả về giá trị .
Bước 2. Điều kiện là n ≥ 0 và theo quy ước thì exp(a,0) = 1 với mọi a. Đây chính là phần cơ sở cho điều kiện dừng của lời gọi đệ quy của hàm exp(a,n).
Bước 3. Ta có suy ra exp(a,n) = a × exp(a,n-1), đây là công thức truy hồi tính exp(a,n). Từ đó có thể thiết lập lời gọi đệ quy của hàm này.
3. Tính n giai thừa n!=1 x 2 x 3 x … x n
Bước 1. Bài toán yêu cầu tính n giai thừa n!. Ta cần thiết lập hàm giaithua(n) trả về giá trị n!.
Bước 2. Điều kiện là n ≥ 0 và quy ước 0! = 1, tức là giaithua (0) = 1. Đây là cơ sở cho điều kiện dừng của lời gọi đệ quy của hàm giaithua(n).
Bước 3. Ta có công thức giaithua(n) = n × giaithua(n-1), đây là công thức truy hồi tính giaithua(n). Từ đó dễ dàng thiết lập lời gọi đệ quy cho hàm này.
Lời giải bài tập Chuyên đề Tin 11 Bài 2: Thiết kế thuật toán đệ quy hay, chi tiết khác: