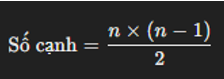Một đơn đồ thị, vô hướng có n đỉnh, có thể có số cạnh lớn nhất là bao nhiêu?
Một đơn đồ thị, vô hướng có n đỉnh, có thể có số cạnh lớn nhất là bao nhiêu?
Giải Chuyên đề Tin 12 Bài 12: Biểu diễn đồ thị - Kết nối tri thức
Câu hỏi 1 trang 61 Chuyên đề Tin học 12: Một đơn đồ thị, vô hướng có n đỉnh, có thể có số cạnh lớn nhất là bao nhiêu?
Lời giải:
Trong một đơn đồ thị vô hướng có n đỉnh, số cạnh lớn nhất có thể có được là khi mỗi cặp đỉnh đều được nối với nhau bằng một cạnh. Điều này xảy ra khi đồ thị là đồ thị đầy đủ.
Một đồ thị đầy đủ có nnn đỉnh sẽ có tất cả các cặp đỉnh đều được nối với nhau bằng một cạnh.
Số cạnh của một đồ thị đầy đủ với n đỉnh được tính bằng công thức sau:
Do mỗi cặp đỉnh được nối với nhau bằng một cạnh, và số lượng cặp đỉnh là
(lấy một đỉnh, sau đó chọn một đỉnh từ n−1 đỉnh còn lại).
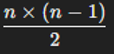
Vì vậy, số cạnh lớn nhất của một đơn đồ thị vô hướng với n đỉnh là
Lời giải bài tập Chuyên đề Tin 12 Bài 12: Biểu diễn đồ thị hay, ngắn gọn khác:
Câu hỏi 1 trang 57 Chuyên đề Tin học 12: Vẽ đồ thị có tệp dữ liệu ma trận kề Hình 12.5 ....
Câu hỏi 2 trang 59 Chuyên đề Tin học 12: Khi nào ma trận kề A chỉ gồm toàn số 0? ....