Cây nhị phân có thể được coi là đồ thị vô hướng, các nút của cây sẽ tương ứng là đỉnh
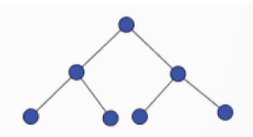
Cây nhị phân có thể được coi là đồ thị vô hướng, các nút của cây sẽ tương ứng là đỉnh, còn quan hệ cha-con là cạnh nối của đồ thị. Với cây nhị phân hoàn chỉnh, các đỉnh được đánh số theo chỉ số của mảng biểu diễn tương ứng của cây. Hãy tính ma trận kề của đồ thị tương ứng cây nhị phân ở hình bên.
Giải Chuyên đề Tin 12 Bài 13: Thực hành thiết lập đồ thị - Kết nối tri thức
Vận dụng 1 trang 64 Chuyên đề Tin học 12: Cây nhị phân có thể được coi là đồ thị vô hướng, các nút của cây sẽ tương ứng là đỉnh, còn quan hệ cha-con là cạnh nối của đồ thị. Với cây nhị phân hoàn chỉnh, các đỉnh được đánh số theo chỉ số của mảng biểu diễn tương ứng của cây. Hãy tính ma trận kề của đồ thị tương ứng cây nhị phân ở hình bên.
Lời giải:
Để tính ma trận kề của đồ thị tương ứng với cây nhị phân hoàn chỉnh, chúng ta cần xác định cách biểu diễn cây nhị phân hoàn chỉnh bằng mảng và sau đó chuyển đổi thông tin này thành ma trận kề. Trong cây nhị phân hoàn chỉnh, mỗi nút được đánh số theo chỉ số của mảng biểu diễn, và quan hệ cha-con được duy trì bằng cách tính toán chỉ số của các nút cha và con.
Dưới đây là cách tính ma trận kề của đồ thị tương ứng với cây nhị phân hoàn chỉnh:
1. Xác định số lượng đỉnh của cây nhị phân hoàn chỉnh. Số lượng đỉnh của cây nhị phân hoàn chỉnh có thể tính bằng công thức 2n−1, trong đó nnn là số tầng của cây.
2. Khởi tạo ma trận kề A với kích thước n×n và tất cả các phần tử đều bằng 0 ban đầu.
3. Duyệt qua từng nút của cây và thiết lập các cạnh nối trong ma trận kề:
- Nếu nút ở vị trí i có con trái (nếu có) ở vị trí 2i+1 và con phải (nếu có) ở vị trí 2i+2, thì đặt A[i][2i+1]=A[i][2i+2]=1 (do đỉnh i kết nối với đỉnh 2i+1 và 2i+2).
- Lưu ý rằng trong trường hợp số lượng đỉnh của cây không phải là một lũy thừa của 2, một số phần tử cuối cùng của mảng biểu diễn cây sẽ không có nút con, do đó cần kiểm tra điều kiện 2i+1 và 2i+2 có vượt quá số lượng đỉnh của cây hay không trước khi gán cạnh nối.
Một ví dụ chương trình Python thực hiện việc tính ma trận kề của đồ thị tương ứng với cây nhị phân hoàn chỉnh:
def calculate_adjacency_matrix_complete_binary_tree(levels):
n = 2 ** levels - 1 # Số lượng đỉnh của cây nhị phân hoàn chỉnh
A = [[0] * n for _ in range(n)] # Khởi tạo ma trận kề
# Thiết lập cạnh nối giữa các đỉnh
for i in range(n):
left_child = 2 * i + 1
right_child = 2 * i + 2
if left_child < n:
A[i][left_child] = 1
if right_child < n:
A[i][right_child] = 1
return A
# Số tầng của cây nhị phân hoàn chỉnh
levels = 3
# Tính ma trận kề của cây nhị phân hoàn chỉnh với số tầng là levels
adjacency_matrix = calculate_adjacency_matrix_complete_binary_tree(levels)
# In ma trận kề
for row in adjacency_matrix:
print(row)
Trong ví dụ này, chúng ta tính ma trận kề cho một cây nhị phân hoàn chỉnh có 3 tầng và in ra ma trận kề tương ứng. Đảm bảo rằng số tầng nnn là số nguyên không âm.
Lời giải bài tập Chuyên đề Tin 12 Bài 13: Thực hành thiết lập đồ thị hay, ngắn gọn khác: