Hoạt động 2 trang 44 Chuyên đề Toán 11 Cánh diều
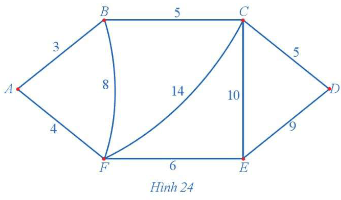
Giả sử có sáu địa điểm A, B, C, D, E, F được nối với nhau theo những con đường với độ dài (đơn vị: kilômét) được mô tả bằng đồ thị có trọng số ở . Người giao hàng cần đi giao hàng tại sáu địa điểm trên. Người giao hàng xuất phát từ một địa điểm nào đó, đi qua các địa điểm còn lại để giao hàng và trở về địa điểm ban đầu. Hãy tìm một đường đi thỏa mãn điều kiện trên cho người giao hàng sao cho quãng đường mà người giao hàng phải di chuyển là ngắn nhất.
Giải Chuyên đề Toán 11 Bài 2: Một vài ứng dụng của lí thuyết đồ thị - Cánh diều
Hoạt động 2 trang 44 Chuyên đề Toán 11: Giả sử có sáu địa điểm A, B, C, D, E, F được nối với nhau theo những con đường với độ dài (đơn vị: kilômét) được mô tả bằng đồ thị có trọng số ở Hình 24. Người giao hàng cần đi giao hàng tại sáu địa điểm trên. Người giao hàng xuất phát từ một địa điểm nào đó, đi qua các địa điểm còn lại để giao hàng và trở về địa điểm ban đầu. Hãy tìm một đường đi thỏa mãn điều kiện trên cho người giao hàng sao cho quãng đường mà người giao hàng phải di chuyển là ngắn nhất.
Lời giải:
Để tìm quãng đường đi ngắn nhất trên đồ thị có trọng số, ta áp dụng thuật toán láng giềng gần nhất để tìm tất cả các chu trình xuất phát từ một đỉnh ban đầu, đi qua các đỉnh khác và trở về đỉnh ban đầu sao cho tổng độ dài các cạnh của chu trình đó là ngắn nhất. Sau đó, ta so sánh độ dài của tất cả các chu trình “tốt nhất” vừa tìm được để tìm ra chu trình có tổng độ dài các cạnh là ngắn nhất. Việc giải cụ thể Hoạt động 2 trang 46, ta cùng xem chi tiết ở Luyện tập 2 trang 46.
Lời giải Chuyên đề Toán 11 Bài 2: Một vài ứng dụng của lí thuyết đồ thị hay, chi tiết khác: