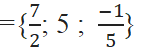Giải các phương trình (3x – 2)(4x + 5) = 0

Bài 4: Phương trình tích

Bài 21 trang 17 Toán 8 Tập 2: Giải các phương trình:

a) (3x – 2)(4x + 5) = 0;                  b) (2,3x – 6,9)(0,1x + 2) = 0;

c) (4x + 2)(x2 + 1) = 0;                   d) (2x + 7)(x – 5)(5x + 1) = 0;

Trả lời

a) (3x – 2)(4x + 5) = 0

⇔ 3x – 2 = 0 hoặc 4x + 5 = 0

1) 3x – 2 = 0 ⇔ 3x = 2 ⇔ x = 2/3

2) 4x + 5 = 0 ⇔ 4x = -5 ⇔ x = - 5/4

Vậy phương trình có tập nghiệm S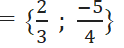

b) (2,3x – 6,9)(0,1x + 2) = 0

⇔ 2,3x – 6,9 = 0 hoặc 0,1x + 2 = 0

1) 2,3x – 6,9 = 0 ⇔ 2,3x = 6,9 ⇔ x = 3

2) 0,1x + 2 = 0 ⇔ 0,1x = -2 ⇔ x = -20.

Vậy phương trình có tập hợp nghiệm S = {3;-20}

c) (4x + 2)(x² + 1) = 0 ⇔ 4x + 2 = 0 hoặc x² + 1 = 0

1) 4x + 2 = 0 ⇔ 4x = -2 ⇔ x = -1/2

2) x² + 1 = 0 ⇔ x² = -1 (vô lí vì x² ≥ 0)

Vậy phương trình có tập hợp nghiệm S ={-1/2}

d) (2x + 7)(x – 5)(5x + 1) = 0

⇔ 2x + 7 = 0 hoặc x – 5 = 0 hoặc 5x + 1 = 0

1) 2x + 7 = 0 ⇔ 2x = -7 ⇔ x = -7/2

2) x – 5 = 0 ⇔ x = 5

3) 5x + 1 = 0 ⇔ 5x = -1 ⇔ x = -1/5

Vậy phương trình có tập nghiệm là S