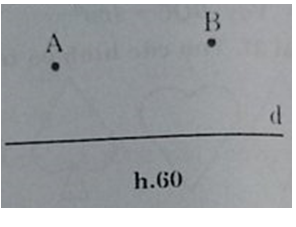
Cho 2 điềm A, B thuộc cùng một mặt phẳng có bờ là đường thẳng d (h.60)

Luyện tập (trang 88-89)

Bài 39 trang 88 Toán 8 Tập 1: a) Cho 2 điềm A, B thuộc cùng một mặt phẳng có bờ là đường thẳng d (h.60). Gọi C là điểm đối xứng với A qua d. Gọi d là giao điểm của đường thẳng d và đoạn thẳng BC. Gọi E là điểm bất kì của đường thẳng d (E khác D).Chứng minh rằng AD + DB < AE +EB

b) Bạn Tú đang ở vị trí A cần đến bờ sông d lấy nước rồi đi đến vị trí B (h.60) con đường ngắn nhất bạn Tú đi là con đường nào

Trả lời

a) A và C đối xứng với nhau qua d, nên AD = CD

⇒ AD + DB = CD + DB = CB (1)

Tương tự như trên ta có:

AE = CE ⇒ AE + CE = CE + EB (2)

Từ tam giác BEC ta có CB < AE + EB (3)

Từ (1) , (2) và (3) suy ra AD + DB < AE+ EB (đpcm)

b) Vì AE + EB > AD + DB

Do đó con đường ngắn nhất mà Tú phải đi là con đường ADB