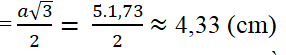Tính diện tích toàn phần của hình chóp tứ giác đều

Luyện tập (trang 124-125)

Bài 48 trang 125 Toán 8 Tập 2: Tính diện tích toàn phần của:

a) Hình chóp tứ giác đều, biết cạnh đáy a = 5cm, cạnh bên b = 5cm, √18,75 ≈ 4,33;

b) Hình chóp lục giác đều, biết cạnh đáy a = 6cm, cạnh bên b = 10cm, √3 ≈ 1,73; √91 ≈ 9,54.

Trả lời

Nhắc lại : Tam giác đều cạnh a thì đường cao h và diện tích S của tam giác đó là:

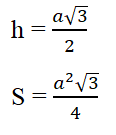
a) Hình chóp tứ giác đều có cạnh đáy là a = 5cm cạnh bên b = 5cm suy ra một mặt bên là tam giác đều cạnh 5cm

Do đó trung đoạn d

Diện tích xung quanh của hình chóp tứ giác đều là:

S_xq = (2x5) x 4,33 ≈ 43,3 (cm²)

Vậy diện tích toàn phần của hình chóp tứ giác đều là:

S_tp = S_xq + S_đáy ≈ 43,3 + 5² ≈ 68,3 (cm²)

b) Tính tương tự như trên ta được

Trung đoạn của hình chóp lục giác đều là d = 4cm

Diện tích xung quanh S_xq = (3x6) x 4 = 72 (cm²)

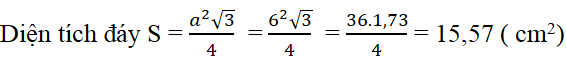
Vậy diện tích toàn phần của hình chóp lục giác đều cạnh đáy a = 6cm cạnh bên 5cm là

Stp ≈ 72 + 15,57 = 87,57 ( cm²)