Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì thuộc cạnh BC

Luyện tập (trang 103)

Bài 71 trang 103 Toán 8 Tập 1: Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE.

a) Chứng minh rằng ba điểm A, O, M thẳng hàng

b) Khi điểm M di chuyển trên cạnh BC thì điểm O di chuyển trên đường nào.

c) Điểm M ở vị trí nào trên cạnh BC thì AM có độ dài nhỏ nhất?

Trả lời

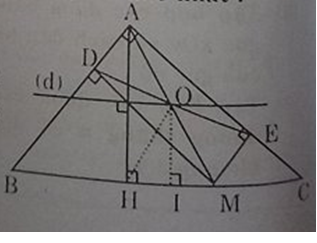
a) Tứ giác ADME có ∠A = ∠D = ∠E = 90º

Vậy nó là hình chữ nhật. Do đó hai đường chéo AM, DE giao nhau tại trung điểm của mỗi đường mà O là trung điểmcủa DE nên AM đi qua O hay 3 điểm A, O, M thẳng hàng

b) – Kẻ đường cao AH của tam giác ABC suy ra độ dài của AH = h không đổi (vì A, B, C cố định)

- Kẻ OI vuông góc BC

Trong tam giác MHA có

⇒ IM = IH

⇒ OI là đường trung bình của tam giác MHA

⇒ OI = 1/2 AH = h/2 không đổi

Vậy khi M di chuyển trên cạnh BC thì điểm O di chuyển trên đoạn thẳng nằm trong tam giác ABC thuộc đường thẳng (d) song song với BC và cách BC một khoảng h/2

c) Ta có

AH là đường vuông góc kẻ từ A đến đường thẳng BC

AM là đường xiên kẻ từ A đến đường thẳng BC

Từ tam giác AHM vuông tại H ta có AM ≥ AH (cạnh huyền lớn hơn cạnh góc vuông)

Vậy AM đạt giá trị nhỏ nhất khi điểm M trùng với chân đường cao kẻ từ đỉnh A, tức là AM = AH