Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng
Bài 1: Bất đẳng thức
Bài 4.1 trang 103 Sách bài tập Đại số 10: Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
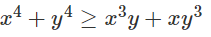
Lời giải:
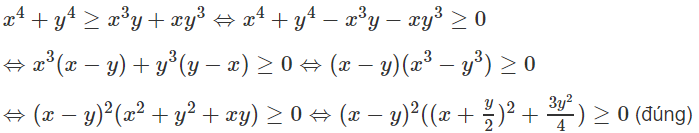
Bài 4.1 trang 103 Sách bài tập Đại số 10: Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
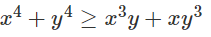
Lời giải:
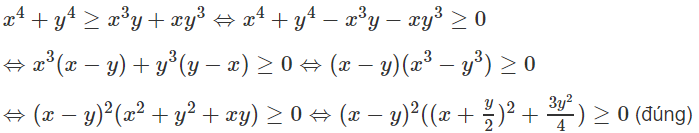
Bài 4.2 trang 103 Sách bài tập Đại số 10: x2 + 4y2 + 3z2 + 14 > 2x + 12y + 6z....
Bài 4.3 trang 104 Sách bài tập Đại số 10: 1/a + 1/b ≥ 4/(a + b)....
Bài 4.4 trang 104 Sách bài tập Đại số 10: 1/a + 1/b + 1/c + 1/d ≥ 16/(a + b + c + d)....
Bài 4.5 trang 104 Sách bài tập Đại số 10: a2b + 1/b ≥ 2a....
Bài 4.6 trang 104 Sách bài tập Đại số 10: (a + b)(b + c)(c + a) ≥ 8abc....
