Chọn khẳng định đúng. Bài tập trắc nghiệm trang 46, 47, 48, 49, 50 Sách bài tập Hình học 10

---

Ôn tập chương 1

Bài tập trắc nghiệm trang 46, 47, 48, 49, 50 Sách bài tập Hình học 10:

    Bài 1.72: Chọn khẳng định đúng:

    A. Hai vectơ có giá trị vuông góc thì cùng phương.

    B. Hai vectơ cùng phương thì giá của chúng song song.

    C. Hai vectơ cùng phương thì cùng hướng.

    D. Hai vectơ ngược hướng với vectơ thứ ba thì ngược hướng.

Lời giải:

Vì hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng.

Đáp án: D

    Bài 1.73: Nếu hai vectơ bằng nhau thì chúng

    A. có độ dài bằng nhau.          B. cùng phương.

    C. cùng điểm gốc.          D. cùng hướng.

Lời giải:

Vì hai vectơ bằng nhau thì cùng độ dài và cùng hướng.

Đáp án: C

    Bài 1.74: Số các vectơ có điểm đầu và điểm cuối là 2 trong 6 điểm phân biệt cho trước là:

    A. 12          B. 21

    C. 27          D. 30

Lời giải:

Với mỗi cặp hai điểm ta có 2 vectơ. Với 6 điểm phân biệt có 15 cặp điểm khác nhau.

Đáp án: D

    Bài 1.75: Số các vectơ có điểm đầu là một trong 5 điểm phân biệt cho trước và có điểm cuối là một trong bốn điểm phân biệt cho trước là:

    A. 20          B. 10

    C. 9          D. 14

Lời giải:

Vì với mỗi điểm trong 5 điểm đầu ta có 4 vectơ.

Đáp án: A

    Bài 1.76: Chọn khẳng định đúng trong các hệ thức sau:

Lời giải:

Áp dụng quy tắc ba điểm

Đáp án: B

    Bài 1.77: Cho các vectơ có cùng độ dài bằng 5 và cùng phương, hãy chọn khẳng định đúng.

    A. Các vectơ đó phải cùng nằm trên một đường thẳng.

    B. Cộng 10 vectơ đôi một ngược hướng ta được vectơ 0.

    C. Cộng 121 vectơ đó ta được vectơ 0

    D. Cộng 25 vectơ đó ta được vectơ có độ dài là 10.

Lời giải:

Tổng hai vectơ đối là 0→.

Đáp án: B

    Bài 1.78: Nếu là các vectơ khác là đối vectơ đối của thì chúng

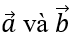
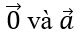
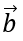
    A. cùng phương.          B. cùng độ dài.

    C. ngược hướng.          D. có chung điểm đầu

    Hãy chọn khẳng định sai.

Lời giải:

Vì hai vectơ đối nhau khi và chỉ khi cùng độ dài và ngược hướng.

Đáp án: D

    Bài 1.79: Vectơ tổng bằng:

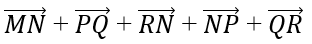
Lời giải:

B

Đáp án: Sử dụng tính chất giao hoán và quy tắc cộng vectơ.

    Bài 1.80: Cho tam giác đều ABC. Hãy chọn đẳng thức đúng.

Lời giải:

Vì AB = AC.

Đáp án: B

    Bài 1.81: Cho hình bình hành ABCD tâm O. Tìm khẳng định sai trong các khẳng định sau:

Lời giải:

Vì AO→ và BO→ không cùng phương.

Đáp án: C

    Bài 1.82: Cho G là trọng tâm của tam giác ABC và I là trung điểm của BC. Hãy chọn đẳng thức đúng.

Lời giải:

Đáp án: B

    Bài 1.83: Cho tam giác ABC, E là điểm trên cạnh BC sao cho BE = BC/4. Hãy chọn đẳng thức đúng.

Lời giải:

Khi phân tích AE→ = hAB→ + kAC→ thì hai số h, k không thể lớn hơn 1, không có số âm và không thể bằng nhau.

Đáp án: B

    Bài 1.84: Cho tam giác ABC, I là trung điểm của BC, M là một điểm tùy ý. Điểm G là trong tâm tam giác ABC nếu:

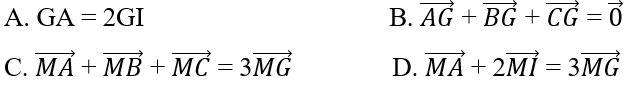
    Hãy chọn khẳng định sai

Lời giải:

Vì G có thể không thuộc AI.

Đáp án: A

    Bài 1.85: Cho hai điểm A, B. Điểm M thuộc đoạn thẳng AB nếu:

    Hãy chọn khẳng định sai.

Lời giải:

Vì từ -3MA→ + 3/4 MB→ = 0 ⃗ suy ra MA→ = 1/4 MB→ mà hai vectơ MA→, 1/4 MB→ ngược hướng.

Đáp án: D

    Bài 1.86: Cho ba điểm không thẳng hàng A, B, C. Điểm D là đỉnh thứ tư của hình bình hành ABCD khi và chỉ khi:

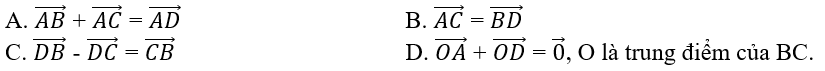
    Hãy chọn khẳng định sai.

Lời giải:

Vì với mọi D đều có DB→ - DC→ = CB→.

Đáp án: C

    Các bài từ 1.87 đến 1.99 xét trong mặt phẳng Oxy

    Bài 1.87: Cho A(-1; 0), B(0; 5), C(3; 1), D(1; -5) và M là một điểm tùy ý. Tọa độ điểm G có tính chất là:

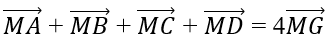
Lời giải:

Vì GA→ + GB→ + GC→ + GD→ = 0 ⃗.

Đáp án: D

    Bài 1.88: Cho . Hãy chọn khẳng định đúng.

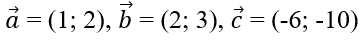
Lời giải:

Đáp án: D

Tính tọa độ của a→ + b→ và a→ - b→. Ta thấy c→ = -2(a→ + b→).

    Bài 1.89: Cho ba điểm A(0; 3), B(1; 5), C(-3; -3). Chọn khẳng định đúng.

    A. A, B, C không thẳng hàng.

    B. A, B, C thẳng hàng.

    C. Điểm B ở giữa A và C.

    

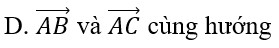
Lời giải:

AB→ = (1;2), AC→ = (-3; -6).

Đáp án: B

    Bài 1.90: Cho tam giác ABC có A(1; -3), B(2; 5), C(0; 7). Trọng tâm của tam giác ABC là điểm có tọa độ:

    A. (0; 5)          B. (1; √2)

    C. (3; 0)          D. (1; 3)

Lời giải:

Tổng ba hoành độ và ba tung độ của ba đỉnh đều khác không và tọa độ không thể là √2.

Đáp án: D

    Bài 1.91: Cho hai điểm A(3; -5), B(1; 7). Chọn khẳng định đúng.

    A. Trung điểm của đoạn thẳng AB có tọa độ là (4; 2).

    B. Tọa độ của vectơ AB là (2; -12).

    C. Tọa độ của vectơ AB là (-2; 12).

    D. Trung điểm của đoạn thẳng AB có tọa độ là (2; -1).

Lời giải:

Vì nếu A(x₁ ; y₁ ), B(x₂ ; y₂ ) thì AB→ = (x₂ - x₁ ; y₂ - y₁ ) và trung điểm I((x₁ + x₂ )/2, (y₁ + y₂ )/2).

Đáp án: C

    Bài 1.92: Cho . Tọa độ của vectơ là:

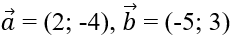
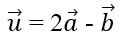
Lời giải:

Sử dụng công thức tọa độ của phép nhân vectơ với một số và phép trừ vectơ.

Đáp án: B

    Bài 1.93: Cho tam giác ABC, trung điểm của các cạnh BC, CA và AB có tọa độ lần lượt là M(1; -1), N(3; 2), P(0; -5). Tọa độ của điểm A là:

    A. (2; -2)          B. (5; 1)

    C. (√5; 0)          D. (2; √2)

Lời giải:

Kiểm tra đẳng thức PA→ = MN→ bằng tọa độ.

Đáp án: A

    Bài 1.94: Cho hình bình hành ABCD có A(-2; 3), B(0; 4), C(5; -4). Tọa độ đỉnh D là:

    A. (√7; 2)          B. (3; -5)

    C. (3; 7)          D. (3; √2)

Lời giải:

Kiểm tra đẳng thức BA→ = CD→ bằng tọa độ.

Đáp án: B

    Bài 1.95: Cho M(5; -3). Kẻ MM₁ vuông góc với Ox, MM₂ vuông góc với Oy. Khẳng định nào đúng?

Lời giải:

Khẳng định đúng là D vì OM→ = OM₁→ + OM₂→ và tọa độ của M là tọa độ của vectơ OM→

Đáp án: D

    Bài 1.96: Cho bốn điểm A(0; 1), B(-1; -2), C(1; 5), D(-1; -1)

    Khẳng định nào đúng?

    A. Ba điểm A, B, C thẳng hàng.

    B. Hai đường thẳng AB và CD song song.

    C. Ba điểm A, B, D thẳng hàng.

    D. Hai đường thẳng AD và BC song song.

Lời giải:

Vì AB→ = (-1; -3), BC→ = (2;7), AD→ = (-1; -2), CD→ = (-2; -6).

Đáp án: B

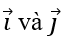
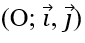
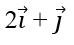
    Bài 1.97: là hai vectơ đơn vị của hệ trục tọa độ . Tọa độ của vectơ là:

    A. (1; -2)          B. (-3; 4)

    C. (2; 1)          D. (0; √3)

Lời giải:

Nhận xét rằng tọa độ của 2i→ + j→ không thể là số âm và số vô tỉ.

Đáp án: C

    Bài 1.98: Cho tam giác ABC có trọng tâm là gốc tọa độ, biết tọa độ hai đỉnh là A(-3; 5), B(0; 4). Tọa độ của đỉnh C là:

    A. (-5; 1)          B. (3; 7)

    C. (3; -9)          D. (√5; 0)

Lời giải:

Tổng các hoành độ và tung độ của ba đỉnh phải bằng 0.

Đáp án: C

    Bài 1.99: Trong mặt phẳng Oxy, cho tam giác đều OAB có AB = 2, AB song song với Ox. Điểm A có hoành độ và tung độ dương. Ta có:

    Hãy chọn khẳng định đúng.

Lời giải:

Vì A, B có cùng tọa độ và hoành độ lần lượt là 1 và -1.

Đáp án: B

    Bài 1.100: Ba lực tác dụng vào một vật có điểm đặt là O và đôi một tạo với nhau góc 120^ο. Với lực F, kí hiệu là cường độ của lực hay độ dài của vectơ lực.

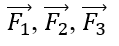
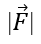
    Vật sẽ chuyển động nếu:

    Hãy chọn khẳng định sai.

Lời giải:

Vì F₁→ + F₂→ là vectơ đối của F₃→.

Đáp án: A