Giải các phương trình sau. Bài 14 trang 218 Sách bài tập Giải tích 12

Ôn tập cuối năm

Bài 14 trang 218 Sách bài tập Giải tích 12: Giải các phương trình sau:

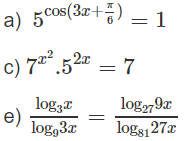
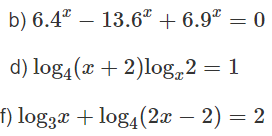
Lời giải:

a) Vì 1 = 5^o nên ta có

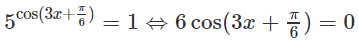
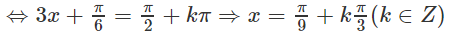
b) 6.4^x − 13.6^x + 6.9^x = 0 (1)

Vì 4^x, 6^x, 9^x đều khác 0 với mọi x ∞ R nên chia cả hai vế của phương trình (1) cho 4^x hoặc 6^x hoặc 9^x , ta được phương trình tương đương.

Chia cả hai vế cho 6^x, ta có: (1)

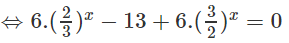
Đặt

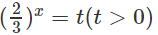
Ta có:

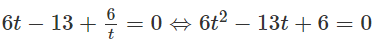
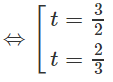
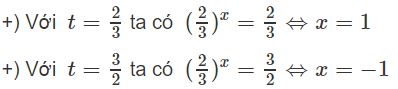
c) Logarit hóa hai vế theo cơ số 7, ta được:

x² + 2x.log₇ 5 − 1 = 0

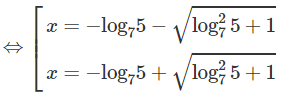
d) log₄(x + 2).log_x2 = 1

Điều kiện:

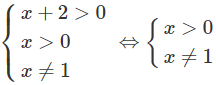
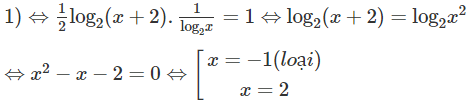
Vậy nghiệm của phương trình là x = 2.

e) Điều kiện: x > 0

Đổi sang cơ số 3 và đặt log₃x = t,

ta được phương trình:

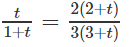
Giải phương trình ẩn t, ta được t₁ = 1, t₂ = −4

Vậy phương trình có hai nghiệm x₁ = 3; x₂ = 1/81

g) Điều kiện:

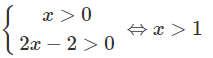
Đặt log₃x + log₄(2x − 2) = f(x)

Dễ thấy f(x) là hàm số đồng biến. Mặt khác f(3) = 2 nên ta có:

f(x) > f(3) = 2 với x > 3 và f(x) < f(3) = 2 với 1 < x < 3.

Từ đó suy ra x = 3 là nghiệm duy nhất.