Cho hai đường thẳng chéo nhau Δ và Δ′ có AA’ là đoạn vuông góc chung, trong đó A ∈ Δ và A′ ∈ Δ′

Bài 2: Mặt cầu

Bài 2.15 trang 60 Sách bài tập Hình học 12: Cho hai đường thẳng chéo nhau Δ và Δ′ có AA’ là đoạn vuông góc chung, trong đó A ∈ Δ và A′ ∈ Δ′. Gọi (α) là mặt phẳng chứa AA’ và vuông góc với Δ′ và cho biết AA’ = a. Một đường thẳng thay đổi luôn luôn song song với mặt phẳng (α) lần lượt cắtΔ và Δ′ tại M và M’ . Hình chiếu vuông góc của M trên mặt phẳng (α) là M₁ .

a) Xác định tâm O và bán kính r của mặt cầu đi qua 5 điểm A, A’ , M , M’, M₁. Tính diện tích của mặt cầu tâm O nói trên theo a, x = A’M’ và góc φ = (Δ, Δ′)

b) Chứng minh rằng khi x thay đổi mặt cầu tâm O luôn luôn chứa một đường tròn cố định.

Lời giải:

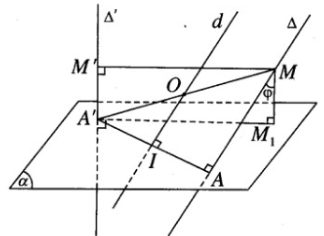
a) Theo giả thiết ta có: ∠A′M′M = ∠A′AM = ∠A′M₁M = 90^o

Do đó 5 điểm A, A’, M, M’, M₁ cùng thuộc mặt cầu (S) tâm O, với O là trung điểm của A’M và có bán kính r = A′M₂

Mặt khác ta có A’M² = A’A² + AM²

Trong đó

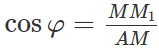
Do đó

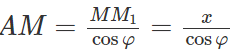
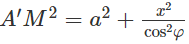
Mặt cầu tâm O có bán kính

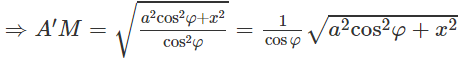
Diện tích của mặt cầu tâm O là:

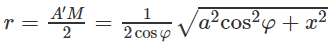
b) Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với Δ. Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.