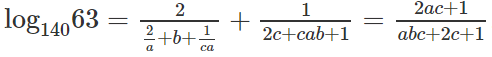Cho a = log3 15, b = log3 10. Hãy tính log√3 50 theo a và b. Cho a = log2 3, b = log3 5, c = log7 2

Bài 3: Lôgarit

Bài 2.17 trang 109 Sách bài tập Giải tích 12: a) Cho a = log₃15, b = log₃10. Hãy tính log_√350 theo a và b.

b) Cho a = log₂3, b = log₃5, c = log₇2. Hãy tính log₁₄₀63 theo a, b, c.

Lời giải:

a) Ta có:

a = log₃15 = log₃(3.5) = log₃3 + log₃5 = 1 + log₃5

Suy ra log₃5 = a – 1

b = log₃10 = log₃(2.5) = log₃2 + log₃5

Suy ra log₃2 = b − log₃5 = b − (a − 1) = b – a + 1

Do đó:

log_√350 = log_3^0,5(2.52) = 2log₃2 + 4log₃5 = 2 (b – a + 1) + 4(a − 1) = 2a + 2b − 2

b) Ta có:

log₁₄₀63 = log₁₄₀(32.7) = 2log₁₄₀3 + log₁₄₀7

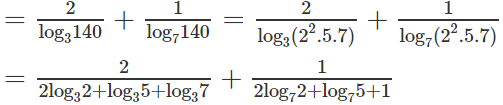
Từ đề bài suy ra:

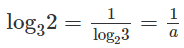
log_0,5π.log₇5 = log₇2.log₂3.log₃₅ = cab

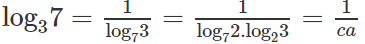
Vậy