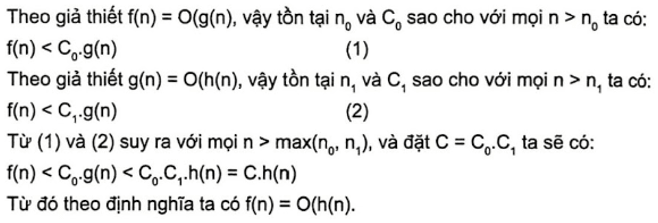Chứng minh rằng nếu f(n) = O(g(n)) và g(n) = O(h(n)) thì ta có: f(n) = O(h(n))
Chứng minh rằng nếu f(n) = O(g(n)) và g(n) = O(h(n)) thì ta có: f(n) = O(h(n)).
Sách bài tập Tin học 11 Bài 24: Đánh giá độ phức tạp thời gian thuật toán - Kết nối tri thức
Câu 24.10 trang 77 SBT Tin học 11: Chứng minh rằng nếu f(n) = O(g(n)) và g(n) = O(h(n)) thì ta có: f(n) = O(h(n)).
Lời giải:
Lời giải sách bài tập Tin học 11 Bài 24: Đánh giá độ phức tạp thời gian thuật toán hay khác:
Câu 24.1 trang 75 SBT Tin học 11: Giả sử một chương trình P mô tả một thuật toán nào đó ....
Câu 24.2 trang 76 SBT Tin học 11: : Đánh giá thời gian chạy của chương trình sau ....
Câu 24.3 trang 76 SBT Tin học 11: Đánh giá thời gian chạy của chương trình sau ....