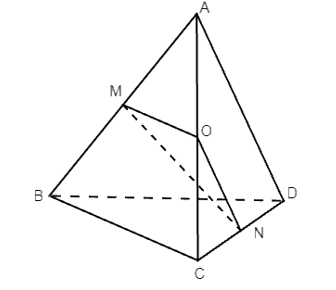
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD

Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tính góc giữa hai đường thẳng AD và BC, biết và AD = BC = 2a.

Giải sách bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc

Bài 5 trang 89 SBT Toán 11 Tập 2: Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tính góc giữa hai đường thẳng AD và BC, biết $MN=a\sqrt{3}$và AD = BC = 2a.

Lời giải:

Gọi O là trung điểm AC.

Do O, M lần lượt là trung điểm AC và AB nên OM là đường trung bình của tam giác ABC.

$\Rightarrow OM=\frac{1}{2}BC=a$ và OM // BC.

Tương tự ta có: ON là đường trung bình của tam giác ACD.

$\Rightarrow ON=\frac{1}{2}AD=a$ và ON // AD.

Khi đó: (AD, BC) = (ON, OM).

Xét tam giác MON, theo hệ quả định lí Cosin ta có:

$\cos \widehat{MON}=\frac{O{M}^2+O{N}^2-M{N}^2}{2OM.ON}=\frac{a^2+a^2-{\left(a\sqrt{3}\right)}^2}{2a.a}=-\frac{1}{2}$.

Nên $\widehat{MON}=120°$.

Suy ra: $\left(AD,BC\right)=\left(ON,OM\right)=180°-\widehat{MON}=180°-120°=60°$.

Vậy góc giữa hai đường thẳng AD và BC là 60°.

Lời giải SBT Toán 11 Bài 1: Hai đường thẳng vuông góc hay khác:

• Bài 1 trang 88 SBT Toán 11 Tập 2: Cho hình lăng trụ ABC.A’B’C’ có ABC là tam giác đều và ABB’A’ là hình chữ nhật. Gọi M là trung điểm của BC (Hình 4). ....

• Bài 2 trang 89 SBT Toán 11 Tập 2: Hình 5 gợi nên hình ảnh một số cặp đường thẳng vuông góc với nhau. Hãy chỉ ra ba cặp đường thẳng vuông góc với nhau.....

• Bài 3 trang 89 SBT Toán 11 Tập 2: Cho hình hộp ABCD.A’B’C’D’ có đáy là hình vuông.....

• Bài 4 trang 89 SBT Toán 11 Tập 2: Cho hình lăng trụ MNPQ.M’N’P’Q’ có tất cả các cạnh bằng nhau. Chứng minh rằng M’N ⊥ P’Q.....