Cho hình chóp S.ABC có SA vuông góc (ABC), đáy là tam giác ABC

Cho hình chóp S.ABC có SA (ABC), đáy là tam giác ABC vuông cân tại B, biết AB = a, SA = a.

Giải sách bài tập Toán 11 Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng - Kết nối tri thức

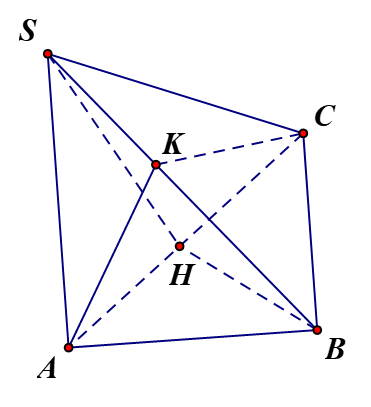
Bài 7.15 trang 30 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA $⊥$ (ABC), đáy là tam giác ABC vuông cân tại B, biết AB = a, SA = a $\sqrt{6}$ .

a) Tính tang của góc giữa đường thẳng SB và mặt phẳng (SAC).

b) Tính sin của góc giữa đường thẳng AC và mặt phẳng (SBC).

Lời giải:

Cho hình chóp S.ABC có SA vuông góc (ABC), đáy là tam giác ABC

a) Kẻ BH $⊥$ AC tại H, mà SA $⊥$ (ABC) nên SA $⊥$ BH nên BH $⊥$ (SAC).

Do đó SH là hình chiếu vuông góc của SB trên mặt phẳng (SAC). Khi đó góc giữa đường thẳng SB và mặt phẳng (SAC) bằng góc giữa hai đường thẳng SB và SH, mà (SH,SB) = $\hat{B S H}$ .

Xét tam giác ABC vuông cân tại B, BH $⊥$ AC, ta có:

$\frac{1}{B H^{2}} = \frac{1}{A B^{2}} + \frac{1}{B C^{2}} = \frac{1}{a^{2}} + \frac{1}{a^{2}} = \frac{2}{a^{2}} \Rightarrow B H = \frac{a \sqrt{2}}{2}$ .

Xét tam giác ABH vuông tại H, có:

AB² = BH² + AH² $\Leftrightarrow$ a² = ${(\frac{a \sqrt{2}}{2})}^{2}$ +AH² $\Leftrightarrow$ AH² = $\frac{a^{2}}{2}$ .

Vì SA $⊥$ (ABC) nên SA $⊥$ AC.

Xét tam giác SAH vuông tại A, có

SA² + AH² = SH² $\Leftrightarrow$ (a $\sqrt{6}$ )² + $\frac{a^{2}}{2}$ = SH² $\Leftrightarrow$ SH = $\frac{a \sqrt{26}}{2}$ .

Vì BH $⊥$ (SAC) nên BH $⊥$ SH.

Xét tam giác SHB vuông tại H, có tan $\hat{B S H}$ = $\frac{H B}{S H}$ = $\frac{\sqrt{13}}{13}$ .

Vậy tang của góc giữa đường thẳng SB và mặt phẳng (SAC) là $\frac{\sqrt{13}}{13}$ .

b) Kẻ AK $⊥$ SB tại K.

Có SA $⊥$ (ABC) nên SA $⊥$ BC mà tam giác ABC vuông tại B nên BC $⊥$ AB.

Do đó BC $⊥$ (SAB) nên BC $⊥$ AK , suy ra AK $⊥$ (SBC).

Do đó CK là hình chiếu vuông góc của AC trên (SBC), suy ra góc giữa đường thẳng AC và mặt phẳng (SBC) bằng góc giữa hai đường thẳng AC và CK, mà (AC,CK) = $\hat{A C K}$ .

Xét tam giác SAB vuông tại A, AK $⊥$ SB, có:

SB = $\sqrt{S A^{2} + A B^{2}} = a \sqrt{7}$ ;

SA.AB = SB.AK $\Rightarrow$ AK = $\frac{S A . A B}{S B}$ = a $\sqrt{\frac{6}{7}}$ .

Do tam giác ABC vuông cân tại B nên AC = $\sqrt{A B^{2} + B C^{2}} = a \sqrt{2}$ .

Vì AK $⊥$ (SBC) nên AK $⊥$ CK.

Xét tam giác ACK vuông tại K, có sin $\hat{A C K} = \frac{A K}{A C} = \sqrt{\frac{3}{7}} = \frac{\sqrt{21}}{7}$ .

Vậy sin của góc giữa đường thẳng AC và mặt phẳng (SBC) là $\frac{\sqrt{21}}{7}$ .

Lời giải SBT Toán 11 Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng hay khác:

Xem thêm lời giải Sách bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯