Ba đường thẳng phân biệt có thể tạo ra bao nhiêu góc? Hãy vẽ hình trong các trường hợp đó

Sách bài tập Toán 6 Bài 6: Góc

Haylamdo biên soạn và sưu tầm lời giải Bài 6 trang 99 sách bài tập Toán lớp 6 Tập 2 sách Chân trời sáng tạo được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 6.

Bài 6 trang 99 sách bài tập Toán lớp 6 Tập 2: Ba đường thẳng phân biệt có thể tạo ra bao nhiêu góc? Hãy vẽ hình trong các trường hợp đó.

Lời giải:

Vẽ hai đường thẳng trước, có hai khả năng xảy ra:

* Khả năng 1: Hai đường thẳng đó song song với nhau.

Ta tiếp tục vẽ thêm một đường thẳng thứ ba song song hoặc cắt cả hai đường thẳng kia.

- Trường hợp 1: Đường thẳng thứ ba song song cả hai đường thẳng kia thì ba đường thẳng này không có giao điểm nào.

Vì ba đường thẳng này không có giao điểm nào nên không có góc nào tạo ra trong trường hợp này.

- Trường hợp 2: Đường thẳng thứ ba cắt cả hai đường thẳng kia thì ta có hai giao điểm A và B.

Từ hai điểm gốc A, B, đặt các tia Aa, Ab, Ac, Bd, Be, Bg (như hình vẽ).

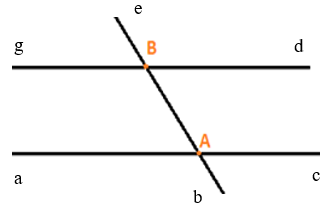
Các góc tạo thành: ∠aAb, ∠bAc, ∠aAe, ∠eAc, ∠aAc, ∠dBe, ∠eBg, ∠dBb, ∠bBg, ∠dBg, ∠bAe, ∠bBe.

Vậy hình trên có 12 góc.

* Khả năng 2: Hai đường thẳng đó cắt nhau cắt nhau tại điểm A.

Ta tiếp tục vẽ thêm một đường thẳng thứ ba cắt cả hai đường thẳng kia.

- Trường hợp 1: Đường thẳng thứ ba cắt cả hai đường thẳng kia và đi qua giao điểm A thì ta có một giao điểm A.

Từ điểm gốc A, đặt các tia Aa, Ab, Ac, Ad, Ae, Ag (như hình vẽ).

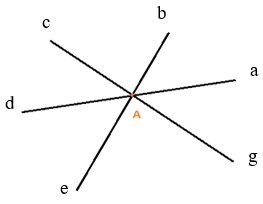
Các góc tạo thành: ∠aAb, ∠bAc, ∠cAd, ∠dAe, ∠eAg, ∠gAa, ∠aAc, ∠cAe, ∠eAa, ∠aAd, ∠bAd, ∠dAg, ∠gAb, ∠bAe, ∠cAg .

Vậy hình trên có 15 góc.

- Trường hợp 2: Đường thẳng thứ ba cắt cả hai đường thẳng kia và không đi qua giao điểm A thì ta có ba giao điểm A, B và C (như hình vẽ).

Từ ba điểm gốc A, B, C đặt các tia Ah, Ak, Bp, Bq, Cm, Cn (như hình vẽ).

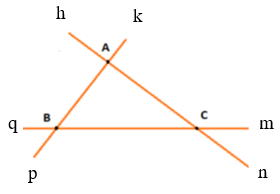
Các góc tạo thành: ∠hAk, ∠kAn, ∠hAp, ∠pAn, ∠hAn, ∠pAk, ∠pBq, ∠pBm, ∠qBk, ∠kBm, ∠mBq, ∠pBk, ∠mCn, ∠mCh, ∠nCq, ∠qCh, ∠nCh, ∠mCq .

Vậy hình trên có 18 góc.

*Nhận xét:

- Hình thứ nhất: Ba đường thẳng không có điểm chung nên không có góc nào tạo ra.

- Hình thứ hai: 2 đỉnh chung, mỗi đỉnh có 4 tia.

Vậy số góc tạo thành là 2 . 4 . 3 : 2 = 12 góc.

- Hình thứ ba: 1 đỉnh chung, có 6 tia.

Vậy số góc tạo thành là 6 . 5 : 2 = 15 (góc).

- Hình thứ tư: 3 đỉnh chung, mỗi đỉnh có 4 tia.

Vậy số góc tạo thành là 3 . 4 . 3 : 2 = 18 (góc).

Vậy nếu đỉnh chung có n tia thì:

Tổng số các góc được tạo thành là: n . (n − 1) : 2 (góc).