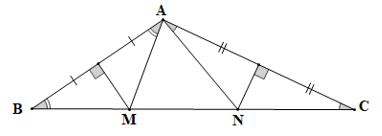
Cho tam giác ABC có góc A bằng 120 độ
Cho tam giác ABC có góc A bằng 120°. Các đường trung trực của AB và AC lần lượt cắt BC tại M và N. Tính số đo góc MAN.
Giải sách bài tập Toán lớp 7 Bài 6: Tính chất ba đường trung trực của tam giác
Bài 3 trang 58 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có góc A bằng 120°. Các đường trung trực của AB và AC lần lượt cắt BC tại M và N. Tính số đo góc MAN.
Lời giải:
Vì M thuộc đường trung trực của AB nên MA = MB.
Do đó tam giác MAB cân tại M.
Suy ra ^MAB=ˆB (tính chất tam giác cân).
Vì N thuộc đường trung trực của AC nên NA = NC.
Do đó tam giác NAC cân tại N.
Suy ra ^NAC=ˆC (tính chất tam giác cân).
Xét ∆ABC có: ︿A+︿B+︿C=180° (định lí tổng ba góc trong một tam giác).
Suy ra ˆB+ˆC=180°−ˆA
Do đó ˆB+ˆC=180°−120°=60°.
Ta có:
^MAN=^BAC−^MAB−^NAC
=^BAC−(^MAB+^NAC)
=120°−(ˆB+ˆC)=120°−60°=60°.
Vậy ^MAN=60°.
