Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, có hai đường phân giác AD

Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, có hai đường phân giác AD, BE cắt nhau tại O. Tính:

Giải SBT Toán 8 Bài 4: Tính chất đường phân giác của tam giác - Cánh diều

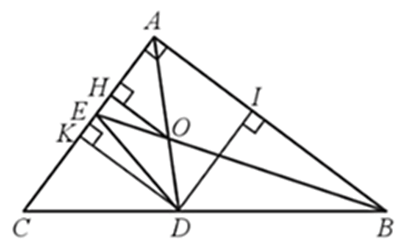
Bài 21 trang 67 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, có hai đường phân giác AD, BE cắt nhau tại O. Tính:

a) Độ dài các đoạn thẳng AE, EC;

b) Khoảng cách từ O đến đường thẳng AC;

c) Độ dài đường phân giác AD (theo đơn vị centimét và làm tròn kết quả đến hàng phần mười);

d) Diện tích tam giác DOE.

Lời giải:

Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, có hai đường phân giác AD

a) Xét ∆ABC vuông tại A nên theo định lí Pythagore, ta có:

BC² = AC² + AB² = 6² + 8² = 100, suy ra BC = 10 (cm).

Xét ∆ABC có BE là phân giác góc ABC nên $\frac{E A}{E C} = \frac{B A}{B C} = \frac{8}{10} = \frac{4}{5}$ (tính chất đường phân giác).

Suy ra $\frac{A E}{4} = \frac{E C}{5} = \frac{A E + E C}{4 + 5} = \frac{A C}{9} = \frac{6}{9} = \frac{2}{3}$

Vậy $A E = 4 \cdot \frac{2}{3} = \frac{8}{3}$ (cm); $E C = 5 \cdot \frac{2}{3} = \frac{10}{3}$ (cm).

b) Kẻ OH ⊥ AC tại H. Khi đó khoảng cách từ O đến đường thẳng AC là độ dài đoạn thẳng OH.

Ta có OH ⊥ AC, AB ⊥ AC nên OH // AB.

Xét ∆ABE với OH // AB, ta có: $\frac{H O}{A B} = \frac{E O}{E B}$ (định lí Thalès) (1).

Xét ∆AEB có AO là phân giác của góc CAB nên $\frac{O E}{O B} = \frac{A E}{A B} = \frac{\frac{8}{3}}{8} = \frac{1}{3}$ (tính chất đường phân giác)

Suy ra $\frac{O E}{O B + O E} = \frac{1}{3 + 1}$ hay $\frac{E O}{E B} = \frac{1}{4}$ (2).

Từ (1) và (2) ta có $\frac{H O}{A B} = \frac{1}{4}$ , suy ra $O H = \frac{1}{4} \cdot A B = \frac{1}{4} \cdot 8 = 2$ (cm).

c) Kẻ DK ⊥ AC, DI ⊥ AB, suy ra $\hat{D K A} = \hat{D I A} = 90 ° .$

Tứ giác AKDI có $\hat{D K A} = \hat{D I A} = \hat{K A I} = 90 °$ nên AKDI là hình chữ nhật

Lại có đường chéo AD là phân giác $\hat{K A I}$ nên AKDI là hình vuông.

Suy ra AK = DK = DI.

Ta có S_∆ABC = S_∆ADC + S_∆ADB nên $\frac{A C \cdot A B}{2} = \frac{A C \cdot D K}{2} + \frac{A B \cdot D I}{2}$

Hay AC.AB = AC.DK + AB.DI = (AB + AC).DK (do DK = DI).

Từ đó, ta có: $D K = \frac{A B \cdot A C}{A B + A C} = \frac{8 \cdot 6}{8 + 6} = \frac{48}{14} = \frac{24}{7} .$

Xét ∆AKC vuông tại K có AD² = AK² + DK² (định lí Pythagore)

Suy ra AD² = AK² + DK² = DK² + DK² = 2DK²

Do đó $A D = D K \sqrt{2} = \frac{24 \sqrt{2}}{7} \approx 4, 8$ (cm).

d) Ta có: $S_{Δ A B C} = \frac{1}{2} A C \cdot A B = \frac{1}{2} \cdot 6 \cdot 8 = 24$ (cm²).

Mà $\frac{S_{Δ B C E}}{S_{Δ B A C}} = \frac{\frac{1}{2} B A \cdot E C}{\frac{1}{2} B A \cdot A C} = \frac{E C}{A C} = \frac{10}{3} : 6 = \frac{5}{9}$

Do đó $S_{Δ B C E} = \frac{5}{9} \cdot S_{Δ B A C} = \frac{5}{9} \cdot 24 = \frac{40}{3}$ (cm²).

Tương tự, ta có: $\frac{S_{Δ B D E}}{S_{Δ B C E}} = \frac{D B}{C B}$

Xét ∆ABC có AD là đường phân giác của góc CAB nên $\frac{D B}{D C} = \frac{A B}{A C}$ (tính chất đường phân giác)

Suy ra $\frac{D B}{D C + D B} = \frac{A B}{A C + A B}$ hay $\frac{D B}{C B} = \frac{8}{8 + 6} = \frac{8}{14} = \frac{4}{7}$

Nên $\frac{S_{Δ B D E}}{S_{Δ B C E}} = \frac{D B}{C B} = \frac{4}{7} .$

Suy ra $S_{Δ BDE} = \frac{4}{7} S_{Δ B C E} = \frac{4}{7} \cdot \frac{40}{3} = \frac{160}{21}$ (cm²)

Lại có $\frac{S_{Δ O D E}}{S_{Δ B D E}} = \frac{O E}{B E} = \frac{1}{4}$

Suy ra $S_{Δ D O E} = \frac{1}{4} \cdot S_{Δ B D E} = \frac{1}{4} \cdot \frac{160}{21} = \frac{40}{21}$ (cm²).

Lời giải SBT Toán 8 Bài 4: Tính chất đường phân giác của tam giác hay khác: