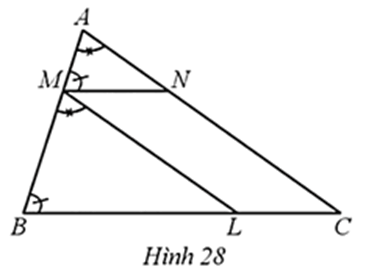
Quan sát Hình 28 biết góc AMN = góc ABC, góc BAC = góc BML
Quan sát biết
Giải SBT Toán 8 Bài 5: Tam giác đồng dạng - Cánh diều
Bài 28 trang 67 SBT Toán 8 Tập 2: Quan sát Hình 28 biết
a) Chứng minh: ∆AMN ᔕ ∆MBL.
b) Xác định vị trí của điểm M trên cạnh AB để chu vi tam giác AMN bằng chu vi tam giác ABC.
Lời giải:
a) Vì và 2 góc này ở vị trí đồng vị nên MN // BC.
Do đó ∆AMN ᔕ ∆ABC (1).
Vì và 2 góc này ở vị trí đồng vị nên ML // AC.
Do đó ∆MBL ᔕ ∆ABC (2).
Từ (1), (2) ta có ∆AMN ᔕ ∆MBL.
b) Giả sử ∆AMN ᔕ ∆ABC với tỉ số đồng dạng k, ta có:
Suy ra = hay
Do đó, để chu vi tam giác AMN bằng chu vi tam giác ABC thì
Ngược lại, dễ thấy nếu thì chu vi tam giác ABC bằng chu vi tam giác ABC.
Vậy vị trí của điểm M trên cạnh AB để chu vi tam giác AMN bằng chu vi tam giác ABC là
Lời giải SBT Toán 8 Bài 5: Tam giác đồng dạng hay khác: