Bài 1.23 trang 32 Toán 12 Tập 1 - Kết nối tri thức
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
Giải Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số - Kết nối tri thức
Bài 1.23 trang 32 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) ; b) .
Lời giải:
a)
1. Tập xác định của hàm số là ℝ\{1}.
2. Sự biến thiên
Có
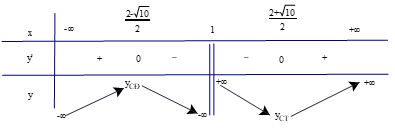
+) Có hoặc .
+) Trên các khoảng và , có y' > 0 nên hàm số đồng biến trên từng khoảng này.
Trên các khoảng và , có y' < 0 nên hàm số nghịch biến trên khoảng này.
+) Hàm số đạt cực cực đại tại và đạt cực tiểu tại .
+) ;
+) Tiệm cận
Do đó x = 1 là tiệm cận đứng của đồ thị hàm số và y = 2x +1 là tiệm cận xiên của đồ thị hàm số.
+) Bảng biến thiên
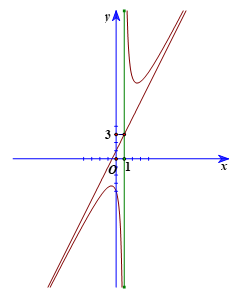
3. Đồ thị
+) Giao điểm của đồ thị hàm số với trục tung là (0; −4).
+) Đồ thị hàm số không cắt trục hoành.
+) Đồ thị hàm số nhận giao điểm I(1; 3) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
b)
1. Tập xác định của hàm số là ℝ\{−3}.
2. Sự biến thiên
Có
+) Có
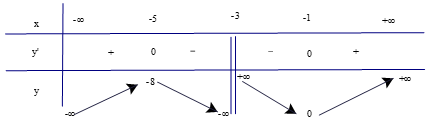
+) Trên các khoảng (−∞; −5) và (−1; +∞), y' > 0 nên hàm số đồng biến trên các khoảng này.
Trên các khoảng (−5; −3) và (−3; −1), y' < 0 nên hàm số nghịch biến trên các khoảng này.
+) Hàm số đạt cực đại tại x = −5 với yCĐ = −8; hàm số đạt cực tiểu tại x = −1 với yCT = 0.
+)
+) Tiệm cận
;
Do đó x = −3 là tiệm cận đứng của đồ thị hàm số và y = x – 1 là tiệm cận xiên của đồ thị hàm số.
+) Bảng biến thiên
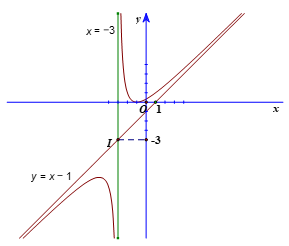
3. Đồ thị
+) Giao điểm của đồ thị với trục tung là
+) Giao điểm của đồ thị với trục hoành là (−1; 0).
+) Đồ thị hàm số nhận giao điểm I(−3; −4) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
Lời giải bài tập Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số hay, chi tiết khác:
HĐ1 trang 26 Toán 12 Tập 1: Cho hàm số y = x2 – 4x + 3. Thực hiện lần lượt các yêu cầu sau ....
Luyện tập 3 trang 32 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số ....