Bài 5 trang 107 Toán 6 Tập 2 Chân trời sáng tạo | Giải Toán lớp 6
Giải Toán lớp 6 Chân trời sáng tạo Bài tập cuối chương 9
Bài 5 trang 107 Toán lớp 6 Tập 2: Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:
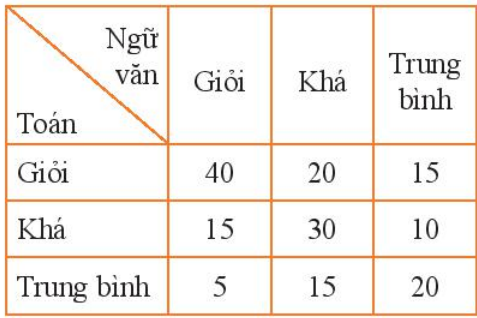
(Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – khá là 20).
Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
a) Môn Toán đạt loại giỏi;
b) Loại khá trở lên ở cả hai môn;
c) Loại trung bình ở ít nhất một môn.
Lời giải:
Tổng số học sinh tham gia kiểm tra là:
40 + 20 + 15 + 15 + 30 + 10 + 5 + 15 + 20 = 170 (học sinh).
a) Số học sinh môn Toán đạt loại giỏi là:
40 + 20 + 15 = 75 (học sinh).
Xác suất thực nghiệm của sự kiện chọn ra học sinh môn Toán đạt loại giỏi là:
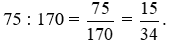
Vậy xác suất thực nghiệm của sự kiện chọn một học sinh được ra một cách ngẫu nhiên có kết quả học sinh môn Toán đạt loại giỏi là 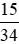 .
.
b) Số học sinh được chọn đạt loại khá trở lên ở cả hai môn bằng tổng số học sinh đạt loại giỏi cả hai môn, giỏi một môn – khá một môn và khá cả hai môn.
Khi đó, số học sinh được chọn đạt loại khá trở lên ở cả hai môn là:
40 + 15 + 20 + 30 =105 (học sinh).
Xác suất thực nghiệm của sự kiện một học sinh được chọn đạt loại khá ở cả hai môn là:
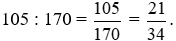
Vậy xác suất thực nghiệm của sự kiện chọn một học sinh được ra một cách ngẫu nhiên có kết quả loại khá ở cả hai môn là 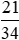 .
.
c) Số học sinh được chọn đạt loại trung bình ở ít nhất một môn, nghĩa là số học sinh đạt loại trung bình một trong hai môn (giỏi một môn – trung bình một môn, khá một môn – trung bình một môn) hoặc đạt loại trung bình cả hai môn.
Do đó, số học sinh đạt loại trung bình ít nhất một môn là:
5 + 15 + 20 + 15 + 10 = 65 (học sinh).
Xác suất thực nghiệm của sự kiện học sinh được chọn đạt loại trung bình ở ít nhất một môn là:
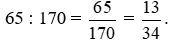
Vậy xác suất thực nghiệm của sự kiện chọn một học sinh được ra một cách ngẫu nhiên có kết quả đạt loại trung bình ở ít nhất một môn là 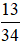 .
.
Lời giải bài tập Toán 6 Bài tập cuối chương 9 hay, chi tiết khác:

