Bài 9 trang 89 Toán 8 Tập 1 Chân trời sáng tạo

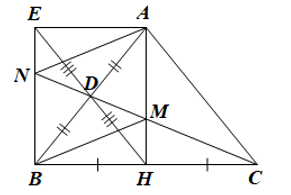
Cho tam giác ABC cân tại A. Gọi H, D lần lượt là trung điểm của các cạnh BC và AB.

Giải Toán 8 Bài tập cuối chương 3 - Chân trời sáng tạo

Bài 9 trang 89 Toán 8 Tập 1: Cho tam giác ABC cân tại A. Gọi H, D lần lượt là trung điểm của các cạnh BC và AB.

a) Chứng minh rằng tứ giác ADHC là hình thang.

b) Gọi E là điểm đối xứng với H qua D. Chứng minh rằng tứ giác AHBE là hình chữ nhật.

c) Tia CD cắt AH tại M và cắt BE tại N. Chứng minh rằng tứ giác AMBN là hình bình hành.

Lời giải:

Bài 9 trang 89 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

a) • Do DABC cân tại A nên $\hat{A B C} = \hat{A C B}$ và AB = AC.

Vì AB = AC nên A nằm trên đường trung trực của BC.

Vì H là trung điểm của BC nên H nằm trên đường trung trực của BC.

Do đó AH là đường trung trực của BC nên AH ⊥ BC.

• Xét DAHB vuông tại H có HD là đường trung tuyến ứng với cạnh huyền AB nên bằng nửa cạnh huyền AB.

Do đó $H D = D B = D A = \frac{1}{2} A B$ .

• Tam giác DBH có DB = DH nên là tam giác cân tại D

Suy ra $\hat{D B H} = \hat{D H B}$ hay $\hat{A B C} = \hat{D H B}$ .

Lại có $\hat{A B C} = \hat{A C B}$ (chứng minh trên) nên $\hat{D H B} = \hat{A C B}$

Mà hai góc này ở vị trí đồng vị nên DH // AC.

• Xét tứ giác ADHC có DH // AC nên là hình thang.

b) Do E là điểm đối xứng với H qua D nên D là trung điểm của HE.

Xét tứ giác AHBE có hai đường chéo AB và HE cắt nhau tại trung điểm D của mỗi đường.

Suy ra AHBE là hình bình hành.

Lại có $\hat{A H B} = 90 °$ (do AH ⊥ BC) nên hình bình hành AHBE là hình chữ nhật.

c) • Do AHBE là hình chữ nhật nên AH // BE hay MH // NE

Suy ra $\hat{M H D} = \hat{N E D}$ (so le trong).

• Xét DMHD và DNED có:

$\hat{M H D} = \hat{N E D}$ (chứng minh trên);

DH = DE (do E là điểm đối xứng với H qua D);

$\hat{H D M} = \hat{E D N}$ (đối đỉnh).

Do đó DMHD = DNED (g.c.g)

Suy ra DM = DN (hai cạnh tương ứng).

Hay D là trung điểm của NM.

• Xét tứ giác AMBN có hai đường chéo AB và NM cắt nhau tại trung điểm D của mỗi đường

Suy ra AMBN là hình bình hành.

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác: