Bài 1 trang 85 Toán 9 Tập 2 Cánh diều

Cho ngũ giác ABCDE có các cạnh bằng nhau và Ngũ giác ABCDE có phải là ngũ giác đều hay không?

Giải Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn - Cánh diều

Bài 1 trang 85 Toán 9 Tập 2: Cho ngũ giác ABCDE có các cạnh bằng nhau và $\widehat{A}=\widehat{B}=\widehat{C}=108°.$ Ngũ giác ABCDE có phải là ngũ giác đều hay không?

Lời giải:

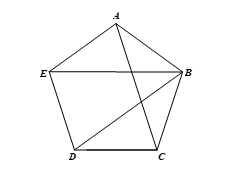
⦁ Do ngũ giác ABCDE có các cạnh bằng nhau nên AB = BC = CD = DE = EA.

Xét ∆ABE có AB = AE nên ∆ABE cân tại A, suy ra $\widehat{ABE}=\widehat{AEB}.$

Lại có $\widehat{BAE}+\widehat{ABE}+\widehat{AEB}=180°$ (tổng ba góc của một tam giác)

Suy ra $\widehat{ABE}=\widehat{AEB}=\frac{180°-\widehat{BAE}}{2}=\frac{180°-108°}{2}=36°.$

Chứng minh tương tự với ∆BCD ta cũng có $\widehat{CBD}=\widehat{CDB}=36°.$

Ta có: $\widehat{ABC}=\widehat{ABE}+\widehat{EBD}+\widehat{DBC}$

Suy ra $\widehat{EBD}=\widehat{ABC}-\widehat{ABE}-\widehat{CBD}=108°-36°-36°=36°.$

⦁ Xét ∆ABE và ∆CDB có:

AB = CD; $\widehat{BAE}=\widehat{DCB}=108°,$ AE = CB

Do đó ∆ABE = ∆CDB (c.g.c)

Suy ra BE = BD (hai cạnh tương ứng)

Nên ∆BDE cân tại B, suy ra $\widehat{BED}=\widehat{BDE}.$

Lại có $\widehat{EBD}+\widehat{BED}+\widehat{BDE}=180°$(tổng ba góc của một tam giác)

Suy ra $\widehat{BED}=\widehat{BDE}=\frac{180°-\widehat{EBD}}{2}=\frac{180°-36°}{2}=72°.$

Khi đó: $\widehat{CDE}=\widehat{CDB}+\widehat{BDE}=36°+72°=108°$

Và $\widehat{AED}=\widehat{AEB}+\widehat{BED}=36°+72°=108°.$

Như vậy, $\widehat{EAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDE}=\widehat{DEA}=108°.$

Vậy ngũ giác ABCDE có 5 cạnh bằng nhau và 5 góc bằng nhau nên ABCDE là ngũ giác đều.

Lời giải bài tập Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn hay, chi tiết khác:

• Khởi động trang 80 Toán 9 Tập 2: Ở lớp dưới, ta đã làm quen với những hình có dạng tam giác đều (Hình 1), hình vuông (Hình 2), lục giác đều (Hình 3)....

• Hoạt động 1 trang 80 Toán 9 Tập 2: Tứ giác MNPQ ở Hình 4a gồm 4 đỉnh M, N, P, Q và 4 cạnh MN, NP, PQ, QM. Ngũ giác ABCDE ở Hình 4b gồm 5 đỉnh A, B, C, D, E....

• Hoạt động 2 trang 81 Toán 9 Tập 2: Nêu đặc điểm về vị trí của ngũ giác ABCDE so với đường thẳng chứa một cạnh bất kì của ngũ giác đó (Hình 5).....

• Hoạt động 3 trang 82 Toán 9 Tập 2: Quan sát Hình 7 và nêu đặc điểm về cạnh và góc của tam giác đều, hình vuông, lục giác đều.....

• Luyện tập trang 83 Toán 9 Tập 2: Ghép sáu miếng phẳng hình tam giác đều có cạnh bằng nhau để tạo thành hình lục giác ABCDEG như ở Hình 10. Lục giác ABCDEG có là lục giác đều hay không....

• Bài 2 trang 85 Toán 9 Tập 2: Bạn Đan gấp một tờ giấy (có dạng hình vuông) lần lượt theo Hình 21a và Hình 21b để được Hình 21c, rồi cắt theo đoạn thẳng màu đỏ như ở Hình 21c....

• Bài 3 trang 85 Toán 9 Tập 2: Hãy tìm hiểu trong tự nhiên hay trong nghệ thuật, trang trí, thiết kế, công nghệ, ... những vật thể mà cấu trúc của nó có dạng hình đa giác đều....

• Bài 4 trang 85 Toán 9 Tập 2: Thiết kế một đồ vật từ những hình có dạng đa giác đều. Chẳng hạn, vẽ trên giấy 20 hình tam giác đều bằng nhau rồi cắt ra ....