Cho tam giác đều ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA

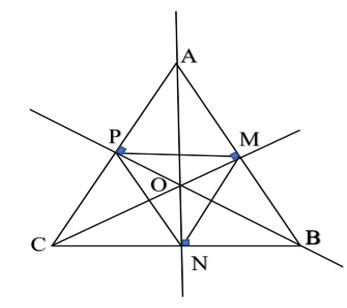
Cho tam giác đều ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA. Hãy vẽ ba đường trung trực của tam giác ABC và ba đường trung trực của tam giác MNP. Có nhận xét gì về giao điểm của ba đường trung trực của tam giác ABC và tam giác MNP.

Giải vở thực hành Toán 7 Bài 6: Tính chất ba đường trung trực của tam giác

Bài 4 trang 52 Vở thực hành Toán 7 Tập 2: Cho tam giác đều ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA. Hãy vẽ ba đường trung trực của tam giác ABC và ba đường trung trực của tam giác MNP. Có nhận xét gì về giao điểm của ba đường trung trực của tam giác ABC và tam giác MNP.

Lời giải:

Tam giác ABC đều nên AB = BC = CA.

Kẻ các đường trung trực của tam giác ABC giao nhau tại O.

M, N, P lần lượt là trung điểm của AB, BC, CA. Suy ra

AM = MB = BN = NC = CP = PA = $\frac{1}{2}$AB = $\frac{1}{2}$BC = $\frac{1}{2}$CA.

Xét tam giác PCO vuông tại P và tam giác NCO vuông tại N.

CP = CN.

Cạnh chung OC.

Vậy tam giác PCO bằng tam giác NCO theo trường hợp cạnh huyền – cạnh góc vuông.

Suy ra OP = ON hay O thuộc đường trung trực của PN. (1)

Xét tam giác OBM vuông tại M và tam giác OBN vuông tại N.

BM = BN.

Cạnh chung OB.

Vậy tam giác OBM bằng tam giác OBN theo trường hợp cạnh huyền – cạnh góc vuông.

Suy ra ON = OM hay O thuộc đường trung trực của MN. (2)

Từ (1) và (2) suy ra O là giao 3 đường trung trực của tam giác MNP ( tính chất ba đường trung trực của tam giác).

Như vậy, giao điểm của ba đường trung trực của tam giác ABC và tam giác MNP trùng nhau.