Một công ty cần tuyển 2 nhân viên. Có 5 người nộp hồ sơ xin việc trong đó có 3 nam và 2 nữ
Một công ty cần tuyển 2 nhân viên. Có 5 người nộp hồ sơ xin việc trong đó có 3 nam và 2 nữ. Vì khả năng của 5 người này như nhau nên công ty chọn ngẫu nhiên lần lượt hai người. Tính xác suất để một nam, một nữ được chọn.
Giải vở thực hành Toán 9 Luyện tập chung trang 77 - Kết nối tri thức
Bài 4 trang 80 VTH Toán 9 Tập 2: Một công ty cần tuyển 2 nhân viên. Có 5 người nộp hồ sơ xin việc trong đó có 3 nam và 2 nữ. Vì khả năng của 5 người này như nhau nên công ty chọn ngẫu nhiên lần lượt hai người. Tính xác suất để một nam, một nữ được chọn.
Lời giải:
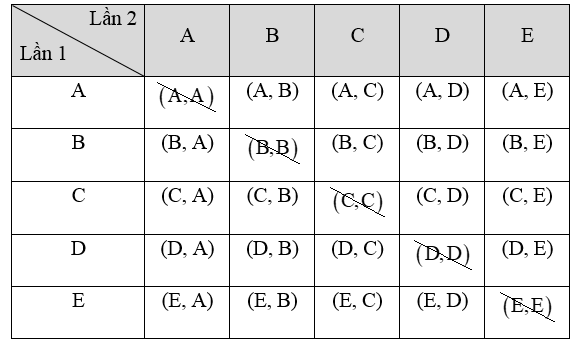
Kí hiệu ba nam là A, B, C và hai nữ là D, E. Mỗi kết quả có thể là cặp (X, Y) trong đó X, Y tương ứng là tên của ứng viên được chọn lần đầu và lần thứ hai với X ≠ Y.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng sau:
Vì X ≠ Y nên cặp có hai phần tử trùng nhau không được tính, tức là trong bảng ta phải xóa 5 ô (A, A); (B, B); (C, C); (D, D); (E, E).
Vậy có 20 kết quả có thể là đồng khả năng.
Có 12 kết quả thuận lợi cho biến cố “chọn được một nam, một nữ” là (A, D); (A, E); (B, D); (B, E); (C, D); (C, E); (D, A); (D, B); (D, C); (E, A); (E, B); (E, C).
Vậy xác suất cần tìm là
Lời giải vở thực hành Toán 9 Luyện tập chung trang 77 hay khác: