Bài 1 trang 66 Chuyên đề Toán 11 Chân trời sáng tạo
Giải Chuyên đề Toán 11 Bài 3: Bài toán tìm đường đi ngắn nhất - Chân trời sáng tạo
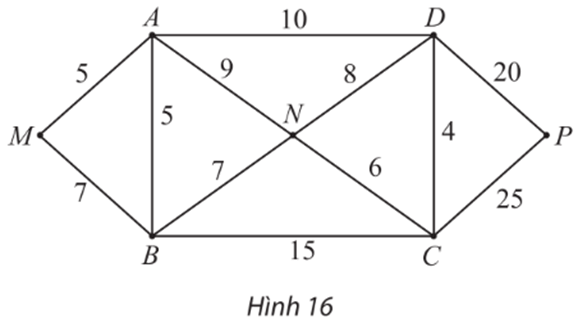
Bài 1 trang 66 Chuyên đề Toán 11: Cho đồ thị có trọng số như Hình 16.
a) Tính độ dài các đường đi ABCD, MBNCP.
b) Chỉ ra ba đường đi khác nhau từ M đến N và tính độ dài của chúng.
c) MBC có phải là đường đi ngắn nhất từ M đến C không?
Lời giải:
a) Ta có:
⦁ lABCD = wAB + wBC + wCD = 5 + 15 + 4 = 24.
⦁ lMBNCP = wMB + wBN + wNC + wCP = 7 + 7 + 6 + 25 = 45.
Vậy độ dài các đường đi ABCD, MBNCP lần lượt là 24 và 45.
b) Ba đường đi khác nhau từ M đến N là: MAN, MBN, MABN.
Ta có:
⦁ lMAN = wMA + wAN = 5 + 9 = 14.
⦁ lMBN = wMB + wBN = 7 + 7 = 14.
⦁ lMABN = wMA + wAB + wBN = 5 + 5 + 7 = 17.
Vậy ba đường đi khác nhau từ M đến N là MAN, MBN, MABN có độ dài lần lượt bằng 14; 14; 17.
c) Ta có MANC là một đường đi từ M đến C.
Mà lMANC = wMA + wAN + wNC = 5 + 9 + 6 = 20 và lMBC = wMB + wBC = 7 + 15 = 22.
Vì 20 < 22 nên lMANC < lMBC.
Vậy MBC không phải là đường đi ngắn nhất từ M đến C.
Lời giải Chuyên đề Toán 11 Bài 3: Bài toán tìm đường đi ngắn nhất hay, chi tiết khác: