Bài 5 trang 66 Chuyên đề Toán 11 Chân trời sáng tạo
Giải Chuyên đề Toán 11 Bài 3: Bài toán tìm đường đi ngắn nhất - Chân trời sáng tạo
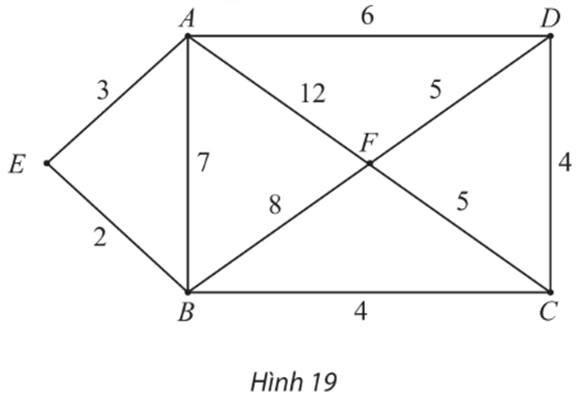
Bài 5 trang 66 Chuyên đề Toán 11: Tìm đường đi ngắn nhất từ đỉnh A đến từng đỉnh (khác A) trong đồ thị có trọng số ở Hình 19.
Lời giải:
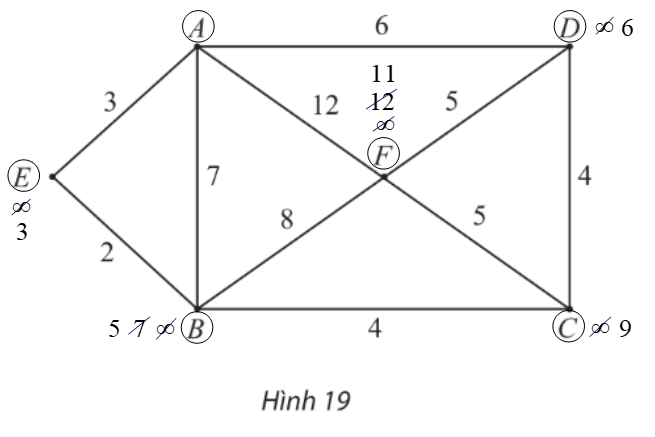
– Gán nhãn cho A bằng 0 (tức là, nA = 0), các đỉnh khác bằng ∞. Khoanh tròn đỉnh A.
– Tại các đỉnh kề với A, gồm E, B, D, F, ta có:
⦁ nE = nA + wAE = 0 + 3 = 3.Vì 3 < ∞ nên ta đổi nhãn của E thành 3.
⦁ nB = nA + wAB = 0 + 7 = 7.Vì 7 < ∞ nên ta đổi nhãn của B thành 7.
⦁ nD = nA + wAD = 0 + 6 = 6.Vì 6 < ∞ nên ta đổi nhãn của D thành 6.
⦁ nF = nA + wAF = 0 + 12 = 12.Vì 12 < ∞ nên ta đổi nhãn của F thành 12.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là E nên ta khoanh tròn đỉnh E (đỉnh gần A nhất, chỉ tính các đỉnh khác A).
Ta có nE = 3 = nA + wAE = wAE = lAE.
Vì vậy AE là đường đi ngắn nhất từ A đến E, với độ dài bằng 3.
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh E chỉ có B, ta có:
nB = nE + wEB = 3 + 2 = 5.Vì 5 < 7 (7 là nhãn hiện tại của B) nên ta đổi nhãn của B thành 5.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần A thứ hai).
Ta có nB = 5 = nE + wEB = nA + wAE + wEB = wAE + wEB = lAEB.
Vì vậy AEB là đường đi ngắn nhất từ A đến B, với độ dài bằng 5.
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh B gồm F, C, ta có:
⦁ nF = nB + wBF = 5 + 8 = 13.Vì 13 > 12 (12 là nhãn hiện tại của F) nên ta giữ nguyên nhãn của F là 12.
⦁ nC = nB + wBC = 5 + 4 = 9.Vì 9 < ∞ nên ta đổi nhãn của C thành 9.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là D nên ta khoanh tròn đỉnh D (đỉnh gần A thứ ba).
Ta có nD = 6 = nA + wAD = wAD = lAD.
Vì vậy AD là đường đi ngắn nhất từ đỉnh A đến D, với độ dài bằng 6.
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh D gồm đỉnh F, C, ta có:
⦁ nF = nD + wDF = 6 + 5 = 11.Vì 11 < 12 (12 là nhãn hiện tại của F) nên ta đổi nhãn của F thành 11.
⦁ nC = nD + wDC = 6 + 4 = 10.Vì 10 > 9 (9 là nhãn hiện tại của C) nên ta giữ nguyên nhãn của C là 9.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là đỉnh C nên ta khoanh tròn đỉnh C (đỉnh gần A thứ tư).
Ta có nC = 9 = nB + wBC
= nE + wEB + wBC
= nA + wAE + wEB + wBC
= wAE + wEB + wBC
= lAEBC.
Vì vậy AEBC là đường đi ngắn nhất từ A đến C, với độ dài bằng 9.
– Lúc này, ta thấy chỉ còn đỉnh F chưa được khoanh tròn nên ta khoanh tròn đỉnh F (đỉnh gần A thứ năm).
Ta có nF = 11 = nD + wDF = nA + wAD + wDF = wAD + wDF = lADF.
Vì vậy ADF là đường đi ngắn nhất từ A đến F, với độ dài bằng 11.
Vậy đường đi ngắn nhất từ đỉnh A đến các đỉnh B, C, D, E, F lần lượt là AEB, AEBC, AD, AE, ADF.
Lời giải Chuyên đề Toán 11 Bài 3: Bài toán tìm đường đi ngắn nhất hay, chi tiết khác: