Bài 2.15 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức
Giải Chuyên đề Toán 11 Bài 10: Bài toán tìm đường tối ưu trong một vài trường hợp đơn giản - Kết nối tri thức
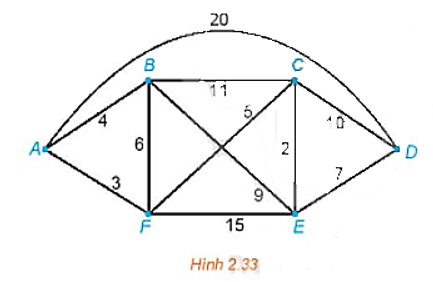
Bài 2.15 trang 49 Chuyên đề Toán 11: Tìm đường đi ngắn nhất từ A đến D trong đồ thị có trọng số trên Hình 2.33.
Lời giải:
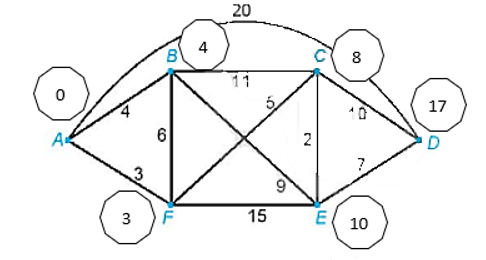
Đầu tiên, ta gắn nhãn đỉnh A là I(A) = 0 và gắn cho ba đỉnh kề với A là B, F và D các nhãn tạm thời I(A) + 4, I(A) + 3 và I(A) + 20. Chọn số nhỏ nhất trong chúng và viết I(F) = 3. Đỉnh F bây giờ được gắn nhãn vĩnh viễn là 3.
Tiếp theo, ta gắn cho các đỉnh kề với F là B, C và E các nhãn tạm thời I(F) + 6, I(F) + 5 và I(F) + 15 (B hiện có hai nhãn tạm thời là 4 và 9). Nhãn tạm thời nhỏ nhất trong các nhãn đã gán (ở B, C, E) hiện nay là 4 (tại B), nên ta viết I(B) = 4. Đỉnh B được gắn nhãn vĩnh viễn là 4.
Bây giờ ta xét các đỉnh kề với B (mà chưa được gắn nhãn vĩnh viễn) là C và E. Ta gắn cho đỉnh C nhãn tạm thời là I(B) + 11 (hiện C có hai nhãn tạm thời là 8 và 15), gắn cho đỉnh E nhãn tạm thời là I(B) + 9 (E hiện có hai nhãn tạm thời là 18 và 13. Nhãn tạm thời nhỏ nhất bây giờ là 8 (tại C), do đó ta viết I(C) = 8.
Bây giờ ta xét các đỉnh kề với C (mà chưa được gắn nhãn vĩnh viễn) là E và D. Ta gắn nhãn cho đỉnh E tạm thời là I(C) + 2 (hiện E có ba nhãn tạm thời là 18, 13 và 10), gắn cho đỉnh D nhãn tạm thời là I(C) + 10. Nhãn tạm thời nhỏ nhất bây giờ là 10 (tại E), do đó ta viết I(E) = 10.
Xét đỉnh kề với E là D, ta gắn cho D nhãn tạm thời I(E) + 7 (hiện D có hai nhãn tạm thời là 18 và 17). Vậy đỉnh D sẽ được gắn nhãn vĩnh viễn là 17 hay I(D) = 17.
Vì I(D) = 17 nên đường đi ngắn nhất từ A đến D có độ dài là 17.
Để tìm một đường đi ngắn nhất từ A đến D như vậy, ta sẽ lần ngược từ điểm cuối D. Ta chỉ cần giới hạn ở việc xét những cạnh mà độ dài là hiệu của các nhãn gắn tại đầu các mút của nó, đó là DE, EC, CF và FA (do I(D) – I(E) = 17 = 10 = 7, I(E) – I(C) = 10 – 8 = 2, I(C) – I(F) = 8 – 3 = 5 và I(F) – I(A) = 3 – 0 = 3).
Khi đó ta có thể kết luận, đường đi ngắn nhất từ A đến D phải đi qua các cạnh DE, EC, CF và FA.
Vậy, đường đi ngắn nhất (trong trường hợp này là duy nhất) từ A đến D là
A → F → C → E → D.
Lời giải bài tập Chuyên đề Toán 11 Bài 10: Bài toán tìm đường tối ưu trong một vài trường hợp đơn giản hay, chi tiết khác: