Bài 3.19 trang 80 Chuyên đề Toán 11
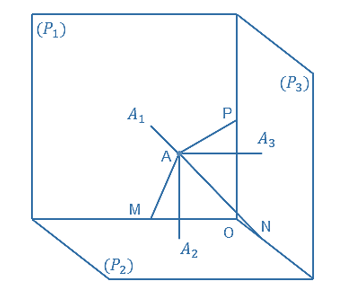
Trong không gian cho điểm A và ba mặt phẳng đôi một vuông góc (P), (P) và (P) giao nhau tại O. Gọi A, A, A lần lượt là hình chiếu vuông góc của A trên các mặt phẳng (P), (P) và (P). Gọi M, N, P lần lượt là chân đường vuông góc hạ từ A xuống các giao tuyến của (P) và (P), (P) và (P), (P) và (P).
Giải Chuyên đề Toán 11 Bài tập cuối chuyên đề 3 - Kết nối tri thức
Bài 3.19 trang 80 Chuyên đề Toán 11: Trong không gian cho điểm A và ba mặt phẳng đôi một vuông góc (P1), (P2) và (P3) giao nhau tại O. Gọi A1, A2, A3 lần lượt là hình chiếu vuông góc của A trên các mặt phẳng (P1), (P2) và (P3). Gọi M, N, P lần lượt là chân đường vuông góc hạ từ A xuống các giao tuyến của (P1) và (P2), (P2) và (P3), (P3) và (P1).
a) Chứng minh OA2 = OM2 + ON2 + OP2.
b) Áp dụng ý a để chứng minh .
Sử dụng kết quả trên để tính độ dài của một đoạn thẳng mà ba hình chiếu có độ dài lần lượt là 1 cm, 2 cm và 3 cm.
Lời giải:
a) Áp dụng định lí Pythagore cho các tam giác vuông.
Tam giác OMA vuông tại M có: OA2 = OM2 + AM2 (1)
Tam giác ONA vuông tại N có: OA2 = ON2 + AN2 (2)
Tam giác OPA vuông tại P có: OA2 = OP2 + AP2 (3)
Cộng vế theo vế của (1), (2), (3) ta được:
3OA2 = (OM2 + ON2 + OP2) + (AM2 + AN2 + AP2)
Ta chứng minh được: AM2 + AN2 + AP2 = 2OA2. (4)
Suy ra: OA2 = OM2 + ON2 + OP2.
b) Vì AM vuông góc OM, OM // AA3 nên AM vuông góc AA3
Mà AA3 vuông góc với OA3
Suy ra: AM // OA3 và AA3 // OM nên AMOA3 là hình bình hành.
Do đó: AM = OA3.
Chứng minh tương tự ta được: AN = OA1, AP = OA2.
Thay kết quả trên vào (4) ta được: .
Suy ra .
Ba hình chiếu có độ dài lần lượt là 1 cm, 2 cm và 3 cm.
Thay số vào kết quả trên ta được: (cm).
Lời giải Chuyên đề Toán 11 Bài tập cuối chuyên đề 3 hay, chi tiết khác: