Bài 5 trang 59 Chuyên đề Toán 11 Chân trời sáng tạo
Giải Chuyên đề Toán 11 Bài 2: Đường đi Euler và đường đi Hamilton - Chân trời sáng tạo
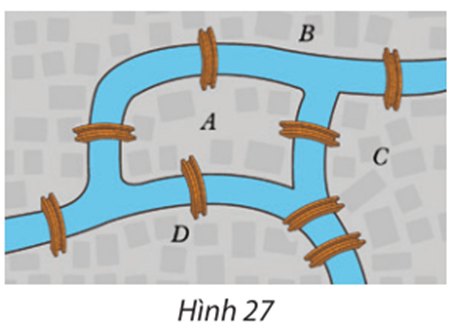
Bài 5 trang 59 Chuyên đề Toán 11: Có bốn khu phố A, B, C và D được nối với nhau bằng những cây cầu như Hình 27. Có hay không cách đi qua tất cả các cây cầu, mỗi cây cầu chỉ qua một lần, rồi quay trở lại nơi xuất phát? Nếu có, hãy chỉ ra một cách đi như vậy.
Lời giải:
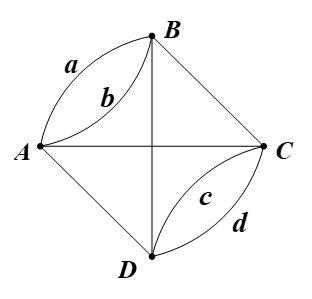
Biểu thị mỗi khu phố bằng một đỉnh, mỗi cây cầu bằng một cạnh nối hai đỉnh, ta được đồ thị như hình vẽ.
Ta có d(A) = d(B) = d(C) = d(D) = 4.
Suy ra tất cả các đỉnh của đồ thị trên đều có bậc chẵn.
Do đó đồ thị trên có chu trình Euler.
Vậy nói cách khác, có cách đi qua tất cả các cây cầu, mỗi cây cầu chỉ qua một lần, rồi quay trở lại nơi xuất phát.
Chẳng hạn, bắt đầu từ đỉnh A, ta có thể đi theo chu trình Euler: AabADcdDBCA.
Lời giải Chuyên đề Toán 11 Bài 2: Đường đi Euler và đường đi Hamilton hay, chi tiết khác: