Bài 2.15 trang 45 Chuyên đề Toán 12

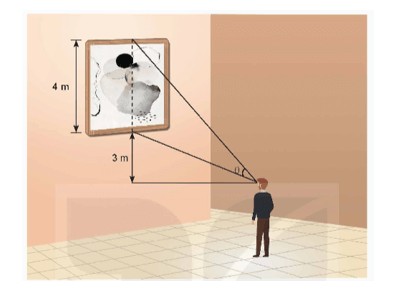
Một bức tranh cao 4 m được treo trên tường có mép dưới cao hơn tầm mắt người quan sát 3 m (như hình vẽ). Người quan sát phải đứng cách tường bao nhiêu mét để có được tầm nhìn thuận lợi nhất (tức là, có góc nhìn θ lớn nhất)?

Giải Chuyên đề Toán 12 Bài tập cuối chuyên đề 2 - Kết nối tri thức

Bài 2.15 trang 45 Chuyên đề Toán 12: Một bức tranh cao 4 m được treo trên tường có mép dưới cao hơn tầm mắt người quan sát 3 m (như hình vẽ). Người quan sát phải đứng cách tường bao nhiêu mét để có được tầm nhìn thuận lợi nhất (tức là, có góc nhìn θ lớn nhất)?

Lời giải:

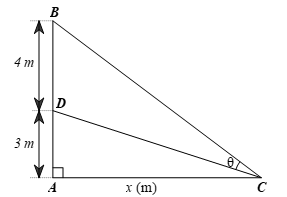
Giả sử tình huống được mô tả bởi hình vẽ dưới đây với C là vị trí mắt của người quan sát, DB = 4 m là chiều cao của bức tranh, AD = 3 m là khoảng cách từ mép dưới của bức tranh đến mắt người quan sát. 

Giả sử AC = x (m) là khoảng cách từ người quan sát đến tường, x > 0.

Khi đó, ta có: $CD=\sqrt{x^2+3^2}=\sqrt{x^2+9}\text{ (m)}$ và $BC=\sqrt{x^2+{\left(3+4\right)}^2}=\sqrt{x^2+49}\text{ (m).}$

Áp dụng hệ quả định lí Cosin vào tam giác BCD, ta có:

$\cos C=\frac{C{D}^2+B{C}^2-B{D}^2}{2CD\cdot BC}$

$=\frac{2x^2+42}{2\sqrt{x^2+9}\cdot \sqrt{x^2+49}}$$=\frac{x^2+21}{\sqrt{x^4+58x^2+441}}.$

Hay $\cos \theta =\frac{x^2+21}{\sqrt{x^4+58x^2+441}}.$

Với θ ∈ (0°; 90°), để góc nhìn θ lớn nhất thì cosθ nhỏ nhất.

Đặt hàm số $f\left(x\right)=\frac{x^2+21}{\sqrt{x^4+58x^2+441}},$ xét trên khoảng (0; +∞).

Khi đó, ta cần tìm giá trị nhỏ nhất của f(x) trên (0; +∞).

Ta có $f^{\text{'}}\left(x\right)=\frac{2x\sqrt{x^4+58x^2+441}-\left(x^2+21\right)\cdot \frac{4x^3+116x}{2\sqrt{x^4+58x^2+441}}}{x^4+58x^2+441}$

$=\frac{2x\left(x^4+58x^2+441\right)-\left(x^2+21\right)\left(2x^3+58x\right)}{\left(x^4+58x^2+441\right)\sqrt{x^4+58x^2+441}}$

$=\frac{16x^3-336x}{\left(x^4+58x^2+441\right)\sqrt{x^4+58x^2+441}}.$

f’(x) = 0 ⇔ 16x³ – 336x = 0 ⇔ x = 0 (loại) hoặc x² = 21

$\iff x=\sqrt{21}$ (do x ∈ (0; +∞)).

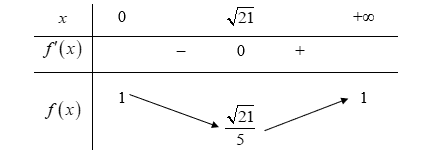
Lập bảng biến thiên của hàm số trên khoảng (0; +∞).

Từ bảng biến thiên, ta có $\underset{\left(0;+\infty \right)}{\min }f\left(x\right)=\frac{\sqrt{21}}{5}$  khi $x=\sqrt{21}\text{.}$

Vậy người quan sát phải đứng cách tường $\sqrt{21}\approx 4,58$  mét để có được tầm nhìn thuận lợi nhất (tức là, có góc nhìn θ lớn nhất).

Lời giải bài tập Chuyên đề Toán 12 Bài tập cuối chuyên đề 2 hay, chi tiết khác:

• Bài 2.11 trang 44 Chuyên đề Toán 12: Một cửa hàng chuyên về cà phê, có sẵn 75 kg cà phê Colombia nguyên chất và 120 kg cà phê thương hiệu của cửa hàng....

• Bài 2.12 trang 44 Chuyên đề Toán 12: Một nhà máy sản xuất hai loại sản phẩm, mỗi sản phẩm yêu cầu sử dụng ba máy. Máy đầu tiên có thể được sử dụng nhiều nhất là 70 giờ, ....

• Bài 2.13 trang 44 Chuyên đề Toán 12: Một công ty bán hàng toàn quốc đang lên kế hoạch tổ chức cuộc họp bán hàng tại Đà Nẵng. Giá vé máy bay khứ hồi thấp nhất từ Hà Nội đến Đà Nẵng là 2 triệu đồng ....

• Bài 2.14 trang 44 Chuyên đề Toán 12: Một vật nặng có khối lượng m được kéo dọc theo mặt phẳng nằm ngang nhờ một sợi dây hợp với phương ngang một góc θ....

• Bài 2.16 trang 45 Chuyên đề Toán 12: Một khu vực hình tròn có bán kính 20 m được bao quanh bởi một lối đi bộ (như hình vẽ). Một bóng đèn được lắp ở trên đỉnh cột nằm ở tâm của khu vực....

• Bài 2.17 trang 45 Chuyên đề Toán 12: Giả sử một loại hàng hoá có hàm cầu được mô hình hoá bởi p = 100 – 0,5x và hàm chi phí được mô hình hoá bởi C = 40x + 37,5, trong đó p (nghìn đồng) ...