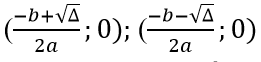Xác định tọa độ giao điểm của parabol y = ax^2 + bx + c với trục tung

Ôn tập chương 2

Bài 7 trang 50 Toán 10: Xác định tọa độ giao điểm của parabol y = ax² + bx + c với trục tung. Tìm điều kiện để parabol này cắt trục hoàn tại hai điểm phân biệt, tại một điểm, và viết tọa độ của các giao điểm trong mỗi trường hợp đó.

Trả lời

* Tọa độ giao điểm của (P): y = ax² + bx + c với trục tung là (0; c)

* Điều kiện để (P) cắt trục hoành tại hai điểm phân biệt là phương trình ax² + bx + c = 0 có biệt số Δ > 0; cắt tại một điểm khi Δ = 0

* Gọi x₁; x₂ là hoành độ giao điểm với tung Ox, ta có

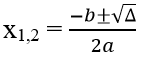
Tọa độ giao điểm là:

* Tọa độ một giao điểm duy nhất là: (- b/2a;0)