Các tam giác ABC cân tại A (A < 90^0). Vẽ BH ⊥ AC (H thuộc AC)

Giải bài tập Toán lớp 7 Luyện tập (trang 137)

Bài 65 trang 137 Toán lớp 7 Tập 1: Các tam giác ABC cân tại A (A < 90⁰). Vẽ BH ⊥ AC (H thuộc AC), CK ⊥ AB (K thuộc AB)

a) Chứng minh rằng AH = AK.

b) Gọi I là giao điểm của BH và CK. Chứng minh rằng tia AI là tia phân giác của góc A.

Trả lời

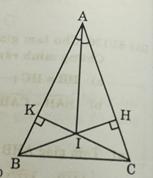
a) Chứng minh AH = AK

Tam giác ABH và tam giác ACK có:

H = K = 90⁰

AB = AC (gt)

BAC góc chung

⇒ ΔABH = ΔACK (ch - gn)

⇒ AH = AK (đpcm)

b) Chứng minh AI là phân giác của

Hai tam giác AIH và AIK có:

H = K = 90⁰

AH = AK (cmt)

AI cạnh chung

⇒ ΔAIH = ΔAIK (ch - gn)

Vậy AI là tia phân giác của góc A.