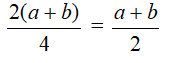Đố. Vẽ hình chữ nhật ABCD có AB = 5cm; BC = 3cm

Luyện tập (trang 119-120)

Bài 15 trang 119 Toán 8 Tập 1: Đố. Vẽ hình chữ nhật ABCD có AB = 5cm; BC = 3cm

a) Hãy vẽ một hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD. Vẽ được mấy hình như vậy?

b) Hãy vẽ hình vuông có chu vi bằng hình chữ nhật ABCD. Vẽ được mấy hình vuông như vậy. So sánh diện tích hình chữ nhật và diện tích hình vuông vừa vẽ. Tại sao trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.

Trả lời

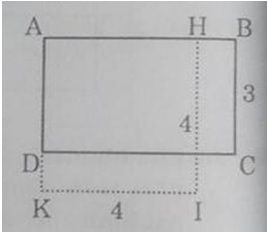
a) Diện tích hình chữ nhật ABCD là

S_ABCD = 3.5 = 15 (cm²)

Và chu vi là CV_ABCD = 2.(5+3) = 16 cm

Chẳng hạn ta vẽ hình chữ nhật BHIK có kích thước 2cm và 7cm thì diện tích S_BHIK = 2.7= 14 (cm2) < S_ABCD

Ta lại có CV_BHIK = 2(2+7) = 18 cm >CV_ABCD

Từ cách vẽ trên ta có thể tìm thêm một số hình chữ nhật có (hai kích thước) như nhau (2cm,7cm) ; (8cm,1cm) ; (7cm,1cm); …

Vậy ta có có thể vẽ được vô số hình chữ nhật có diện tích bé hơn nhưng chu vi lớn hơn hình chữ nhật ABCD

b) Chẳng hạn ta vẽ được hình vuông AHIK có chu vi bằng chu vi của hình chữ nhật ABCD là 16 cm

Ta có CV_AIHK = 4.AH = 16 (cm)

⇒AH = 16 : 4 = 4(cm)

⇒ S_BHIK = 4 . 4 = 16 (cm²) > S_ABCD

Vậy trong các hình chữ nhật có cùng chu vi thì hình vuông (hình chữ nhật đặc biệt) có diện tích lớn nhất.

Thật vậy, nếu hình chữ nhậtcó kích thước là a, b thì diện tích:

S₁ = a.b (1)

Chu vi = 2(a+b)

Một hình vuông có chu vi bằng chu vi hình chữ nhật thì cạnh hình vuông đó là

Như vậy diện tích của hình vuông là

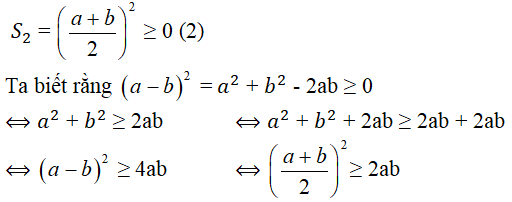
Đối chiều kết quả này với (1), (2) rõ ràng diện tích hình vuông lớn hơn diện tích hình chữ nhật có cùng chu vì

Từ đó ta có thể vẽ được nhiều hình vuông thỏa mãn điều kiện