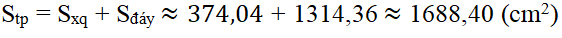S.MNOPQR là một hình chóp lục giác đều Bán kính đường tròn ngoại tiếp
Bài 9: Thể tích của hình chóp đều
Bài 46 trang 124 Toán 8 Tập 2: S.MNOPQR là một hình chóp lục giác đều (h.132). Bán kính đường tròn ngoại tiếp đáy (đường tròn tâm H, đi qua sáu đỉnh của đáy) HM = 12cm (h.133), chiều cao SH = 35cm. Hãy tính:
a) Diện tích đáy và thể tích của hình chóp (biết √108 ≈ 10,39);
b) Độ dài cạnh bên SM và diện tích toàn phần của hình chóp (biết √1333 ≈ 36,51).
Trả lời
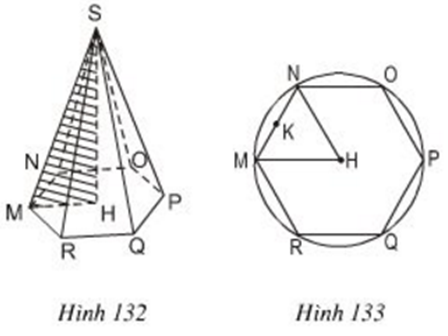
a) Theo tính chất của lục giác đều trong hình 133 tam giác MHN là một trong sáu tam giác đều tạo bởi các đường chéo của lục giác đều đó.
Tương tự bài 45 ta có đường cao:
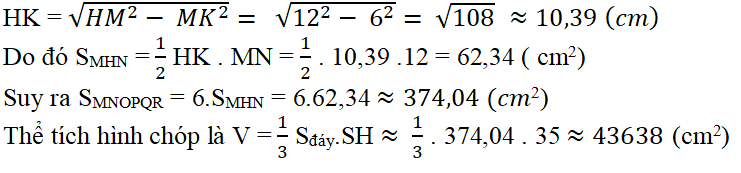
b) Áp dụng định lí Pi – ta-go vào tam giác SHM vuông tại H ta có
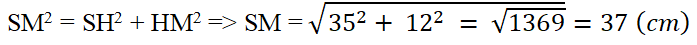
Vậy SM = 37 cm
Ta có K là trung điểm của MN nên SK là trung đoạn của hình chóp. Từ tam giác SKM vuông tại K suy ra:
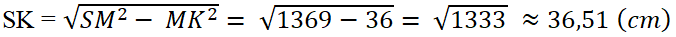
Diện tích xung quanh của chóp đều S.MNOPQR là:
Sxq = p.d = 3.MN.SK = 3.12.36,51 = 1314,36 (cm2)
Vậy diện tích toàn phần của chóp đều S.MNOPQR là :