Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua A, gọi F là điểm xứng

Bài 8: Đối xứng tâm

Bài 52 trang 96 Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua A, gọi F là điểm xứng với D qua C. Chứng minh rằng điểm E đối xứng với điểm F qua B

Hướng dẫn: Muốn có E và F đối xứng qua B ta chứng minh E, B, F thẳng hàng và BE = BF

Trả lời

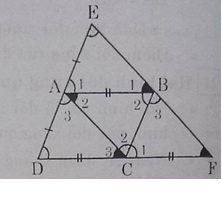
Tứ giác ABCD là hình bình hành ⇒AB // CD và AB = CD

Do AB // CD ⇒∠A₁ = ∠D (đồng vị)

Hai tam giác EAB và ADC có:

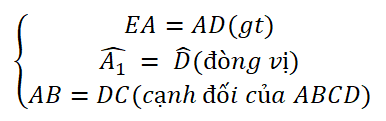
Do đó ΔADC (c.g.c)

BE = AC và ∠A₃ = ∠E ⇒BE // AC ⇒∠A₂ = ∠B₁ (sole trong)

Tương tự, ta có ΔBCF = ΔADC ⇒BF = AC và ∠C₃ = ∠F

⇒BF // AC ⇒∠C₂ =∠B₃ (sole trong)

Từ tam giác ABC có ∠A₂ + ∠B₂ + ∠C₂= 180° do ∠A₂ = ∠B₁ ; ∠C₂=∠B₃ (cmt)

⇒∠B₁ + ∠B₂+ ∠B₃= 180° ⇒E, B, F thẳng hàng (1)

BE = AC và BF = AC, ta suy ra BE = BF (2)

Từ (1) và (2) suy ra E đối xứng với F qua B