Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox

Luyện tập (trang 96)

Bài 54 trang 96 Toán 8 Tập 1: Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, gọi C là điểm đói xứng với A qua Oy. Chứng minh rằng điểm B đối xứng với C qua O.

Trả lời

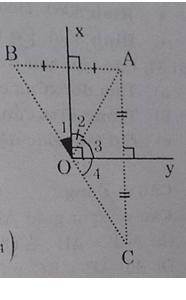
Do A và B đối xứng nhau qua đường thẳng Ox nên Ox là đường trung trực của đoạn thẳng AB ⇒ OA = OB   (1)

Tam giác AOB cân tại O nên õ cũng là phân giác AOB hay ∠O₁ =∠O₂ (2)

Tương tự, Oy là trung trực của đoạn AC ⇒ OC = OA (3)

Tam giác AOC cân tại O nên Oy là phân giác của AOC hay ∠O₃ =∠O₄(4)

Từ (1) và (3) suy ra OB = OC (=OA) (5)

Từ (2) và (4) ⇒ ∠BOC = ∠O₁ + ∠O₂ + ∠O₃ + ∠O₄ = 2 (∠O₃+∠O₄)

Mà ∠O₃ + ∠O₄ = 90º (gt)

Nên ∠BOC = 90º x 2 = 180º

Do đó ba điểm B, O, C thẳng hàng (6)

Từ (5) và (6) suy ra B và C đối xứng nhau qua O.