Cho hình bình hành ABCD, O là giao điểm của hai đường chéo

Luyện tập (trang 96)

Bài 55 trang 96 Toán 8 Tập 1: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M, N. Chứng minh rằng điểm M đối xứng với điểm N qua O

Trả lời

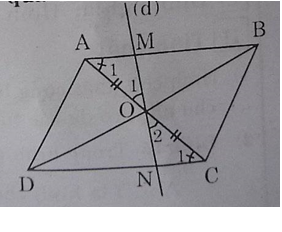
Xét hai tam giác AOM và CON có:

∠O₁= ∠O₂ (đối đỉnh)

OB = OD (do O là giao điểm hai đường chéo hình bình hành ABCD)

∠A₁= ∠C₁ (sole trong)

⇒ ΔAOM = ΔCON ⇒OM = ON

Ta còn có M, N, O đều thuộc đường thẳng (d) (gt)

Vậy M và N đối xứng với nhau qua O