Để chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau, người ta đã làm như hình 15

Bài 2: Định lí đảo và hệ quả của định lí Ta-lét

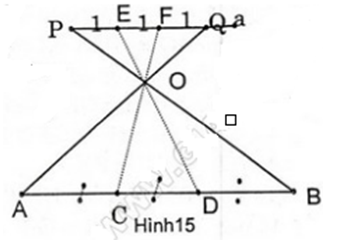
Bài 8 trang 63 Toán 8 Tập 2: a) Để chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau, người ta đã làm như hình 15.

Hãy mô tả cách làm trên và giải thích vì sao các đoạn thẳng AC, CD, DB bằng nhau?

b) Bằng cách làm tương tự, hãy chia đoạn thẳng AB cho trước thành 5 đoạn bằng nhau. Hỏi có cách nào khác với cách làm như trên mà vẫn có thể chia đoạn thẳng AB cho trước thành 5 đoạn thẳng bẳng nhau?

Trả lời

a) Chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau AC = CD = DB

Mô tả : Kẻ đường thẳng a // AB. Trên đường thẳng a đặt 3 đoạn thẳng bẳng nhau và liên tiếp nhau: PE = EF = FQ = 1 (đvdd). Hai đoạn thẳng PB và QA cắt nhau tại O. Kẻ tia EO cắt AB tại D và kẻ tia FO cắt AB tại C.

Do đường thẳng a song song với AB nên theo hệ quả của định lí Ta –let ta có

Mà EF = PE = FQ ( theo cách dựng)

Vậy AC = CD = DB

b) Chia đoạn thẳng AB thành 5 đoạn thẳng bằng nhau

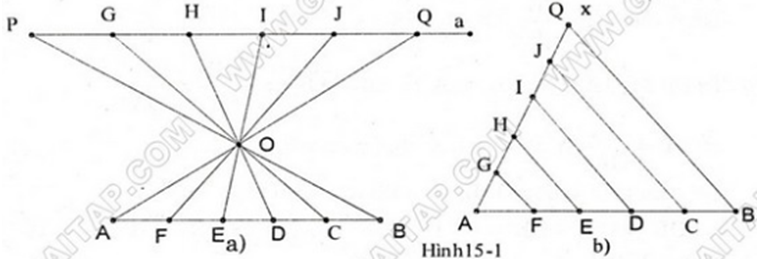
Cách 1: Kẻ đường thẳng a //AB và trên a ta đặt liên tiếp 5 đoạn thẳng bằng nhau HI = IK = KL = LM = MN

Hai đoạn HB và AN cắt nhau tại O. Kẻ các tia IO, KO, LO, MO cắt AB theo thứ tự tại F, E, D, C. Chứng minh tương tự a) ta có năm đoạn thẳng bằng nhau đó là : AC = CD = DE = EF = FB

Cách 2: Kẻ tia Ax. Trên tia Ax đặt năm đoạn thẳng có độ dài bằng nhau AL = LM = MN = NP = PQ

Nối QB. Qua các điểm L, M, N , P ta kẻ các đường thẳng song song với QB. Các đường thẳng này sẽ chia AB thành năm đoạn thẳng bằng nhau