Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA

Ôn tập chương 1 phần hình học

Bài 88 trang 111 Toán 8 Tập 1: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD có điều kiện gì thì EFGH là:

a) Hình chữ nhật?

b) Hình thoi?

c) hình vuông.

Trả lời

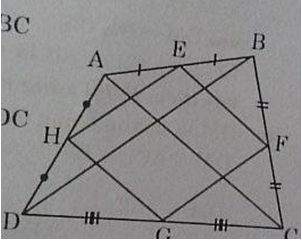
Ta có:

EF là đường trung bình của tam giác ABC

⇒ EF // AC và EF = 1/2 AC

HG là đường trung bình của tam giác ADC

⇒HG // AC và HG = 1/2 AC

Từ hai kết quả trên, suy ra EF // HG và EF = HG

Vậy tứ giác EFGH là hình bình hành

a) Hình bình hành EFGH là hình chữ nhật khi nó có một góc vuông chẳng hạn

∠AEF= 90º ⇒ EH ⊥ EF (1)

Ta có: EH // BD (2)

EF // AC (3)

Từ (1), (2), (3) suy ra AC ⊥ BD

Vậy nếu tứ giác ABCD có hai đường chéo vuông góc với nhau thì EFGH là hình chữ nhật

b) Hình bình hành EFGH là hình thoi khi nó có hai cạnh kề bằng nhau

EF = EH mà EF = 1/2 AC và EH = 1/2 BD ⇒ AC = BD

Vậy nếu tứ giác ABCD có hai đường chéo bằng nhau thì EFGH là hình thoi

c) EFGH là hình vuông khi nó vừa là hình chữ nhật, vừa là hình thoi, suy ra khi tứ giác ABCD có hai đường chéo vuông góc với nhau và bằng nhau thì tứ giác EFGH là hình vuông