Cho tam giác ABC vuông tại A, trung tuyến AM

Ôn tập chương 1 phần hình học

Bài 89 trang 111 Toán 8 Tập 1: Cho tam giác ABC vuông tại A, trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D

a) Chứng minh rằng điểm E đối xứng với điểm M qua AB

b) Các tứ giác AEMC, AEBM là hình gì? Vì sao?

c) Cho BC = 4cm, tính chu vi tứ giác AEBM

d) Tam giác vuông ABC có điều kiện gì thì AEBM là hình vuông?

Trả lời

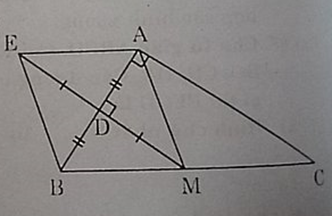
a) Ta phải chứng minh AB là trung trực của ME để suy ra E và M đối xứng nhau qua AB

Ta có MB = MC (gt) và DB = DA (gt)

⇒ MD là đường trung bình cảu tam giác BAC

⇒ MD // AC

Mà AC ⊥ AB (gt) ⇒MD ⊥ AB (1)

Do M và E đối xứng với nhau qua D nên DM = DE (2)

Từ (1) và (2) ⇒ AB là đường trung trực đoạn thẳng EM

Vậy điểm E đối xưng với điểm M qua AB

b) DM là đường trung bình cua rtam giác AB

DM // AC ⇒ EM // AC

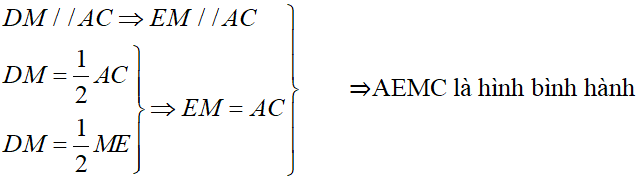
Ta có tứ giác AEBM có hai đường chéo cắt nhau tại trung điểm mỗi đường nên nó là hình bình hành, mặt khác hai đường chéo của AEBM lại vuông góc với nhau. Vậy AEBM là hình thoi.

c) Ta có BC = 4 cm ⇒ BM = 2cm mà AEBM là hình thoi (cmt)

Suy ra cv (AEBM) = 4.BM = 8cm

d) Hình thoi AEBM trở thành hình vuông khi nó có hai đường chéo bằng nhau. Lúc đó AB = EM mà EM = AC ⇒ AB = AC

Vậy tam giác ABC vuông cân tại A thì AEBM là hình vuông