Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng. y = -2x + 3 trên R

Bài 1: Hàm số

Bài 2.5 trang 31 Sách bài tập Đại số 10: Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng

    a) y = -2x + 3 trên R

    b) y = x² + 10x + 9 trên (-5; +∞)

    c) trên (-3; 2) và (2; 3)

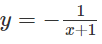
Lời giải:

    a) ∀ x₁, x₂ ∈ R ta có:

    f(x₁) - f(x₂) = -2x₁ + 3 - (-2x₂ + 3) = -2(x₁ - x₂)

    Ta thấy x₁ > x₂ thì 2(x₁ - x₂) < 0 tức là:

    f(x₁) - f(x₂) < 0 ⇔ f(x₁) &ly; f(x₂)

    Vậy hàm số đã cho nghịch biến trên R.

    b) ∀ x₁, x₂ ∈ R ta có:

    f(x₁) - f(x₂) = x₁² + 10x₁ + 9 - x₂² - 10x₂ - 9

    = (x₁ - x₂)(x₁ + x₂) + 10(x₁ - x₂)

    = (x₁ - x₂)(x₁ + x₂ + 10) (∗)

    ∀ x₁, x₂ ∈ (-5; +∞) và x₁ < x₂ ta có x₁ - x₂ < 0 và x₁ + x₂ + 10 > 0 vì

    x₁ > -5; x₁ > -5; ⇒ x₁ + x₂ > -10

    Vậy từ (∗) suy ra f(x₁) - f(x₂) < 0 ⇔ f(x₁) < f(x₂)

    Hàm số đồng biến trên khoảng (-5; +∞)

    c) ∀ x₁, x₂ ∈ (-3; -2) và x₁ < x₂, ta có:

     x₁ - x₂ < 0;

     x₁ + 1 < -2 + 1 < 0;

     x₂ + 1 < -2 + 1 < 0;

    ⇒ (x₁ + 1)(x₂ + 1) > 0.

    Vậy

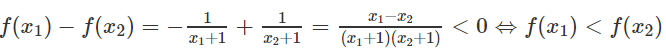
    Do đó hàm số đồng biến trên khoảng (-3; -2)

    ∀ x₁, x₂ ∈ (-3; -2) và x₁ < x₂ tương tự ta cũng có f(x₁) < f(x₂)

    Vậy hàm số đồng biến trên khoảng (2;3).