Cho tam giác ABC có A(-2; 3) và hai đường trung tuyến: 2x - y + 1 = 0 và x + y - 4 = 0

Bài 1: Phương trình đường thẳng

Bài 3.7 trang 148 Sách bài tập Hình học 10: Cho tam giác ABC có A(-2; 3) và hai đường trung tuyến: 2x - y + 1 = 0 và x + y - 4 = 0. Hãy viết phương trình ba đường thẳng chứa ba cạnh của tam giác.

Lời giải:

    Hai đường trung tuyến đã cho đều không phải là đường trung tuyến xuất phát từ A vì tọa độ A không thỏa mãn các phương trình của chúng. Đặt BM: 2x - y + 1 = 0 và CN: x + y - 4 = 0 là hai trung tuyến của tam giác ABC.

    Đặt B(x;y), ta có và

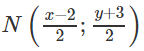
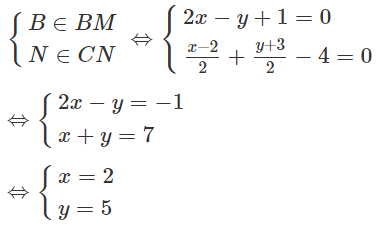
    Vậy phương trình đường thẳng chứa cạnh AB là : 2x - 4y + 16 = 0

    ⇔ x - 2y + 8 = 0

    Tương tự ta có phương trình đường thẳng chứa cạnh AC là : 2x + 5y - 11 = 0

    Phương trình đường thẳng chứa cạnh BC là : 4x + y - 13 = 0