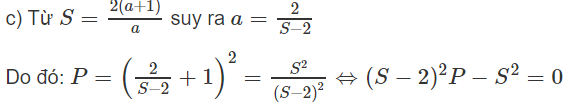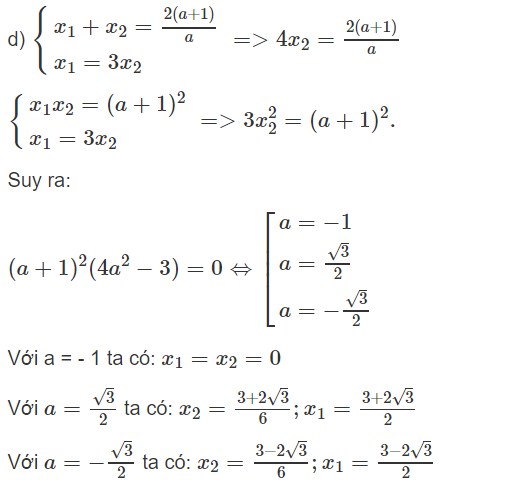Cho phương trình bậc hai ax^2 - 2(a + 1)x + (a + 1)^2a = 0 (E) Kí hiệu S là tổng, P là tích các nghiệm

Ôn tập cuối năm

Bài 8 trang 212 Sách bài tập Đại số 10: Cho phương trình bậc hai

    ax² - 2(a + 1)x + (a + 1)²a = 0 (E)

    Kí hiệu S là tổng, P là tích các nghiệm (nếu có) của phương trình trên.

    a) Với giá trị nào của a, phương trình (E) có nghiệm?

    b) Biện luận dấu của S và P. Từ đó suy ra dấu các nghiệm của (E).

    c) Tìm hệ thức giữa S và P độc lập đối với a.

    d) Với những giá trị nào của a, các nghiệm x₁, x₂ của (E) thỏa mãn hệ thức x₁ = 3x₂? Tìm các nghiệm x₁, x₂ trong mỗi trường hợp đó.

Lời giải:

    a) Phải có:

    Δ = (a + 1)² - (a + 1)²a² = (a + 1)²(1 - a²) ≥ 0

    ⇔ -1 ≤ a ≤ 1, a ≠ 0

    b) Ta có:

    P = (a + 1)²

    P = 0 ⇔ a = -1, khi đó x₁ = x₂ = 0

    P > 0, ∀a ≠ -1 khi đó x₁, x₂ cùng dấu.

    Mặt khác

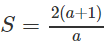
    Suy ra:

    Với 0 < a ≤ 1 thì hai nghiệm của phương trình (E) đều dương;

    Với -1 ≤ a < 0 thì hai nghiệm của phương trình (E) đều âm;