Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l

Bài 1: Khái niệm về mặt tròn xoay

Bài 2.1 trang 46 Sách bài tập Hình học 12: Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng α

a) Tính diện tích xung quanh của hình nón và thể tích khối nón được tạo nên.

b) Gọi I là một điểm trên đường cao DO của hình nón sao cho . Tính diện tích thiết diện qua I và vuông góc với trục của hình nón.

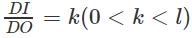
Lời giải:

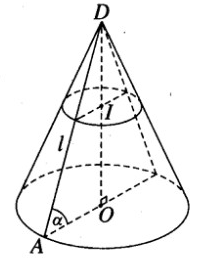
a) Gọi r là bán kính của đường tròn đáy.

Ta có OA = r = l.cosα (với O là tâm của đường tròn đáy và A là một điểm trên đường tròn đó).

Ta suy ra: S_xq = πrl = πl²cosα

Khối nón có chiều cao h = DO = lsinα. Do đó thể tích V của khối nón được tính theo công thức

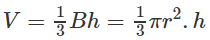
Vậy :

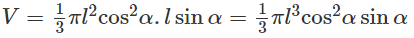
b) Thiết diện qua I và vuông góc với trục hình nón là một hình tròn bán kính r’

với

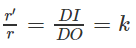
Gọi s là diện tích của thiết diện và S là diện tích của đáy hình tròn ta có:

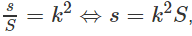
trong đó S = πr² = πl²cos2α

Vậy diện tích của thiết diện đi qua điểm I và vuông góc với trục hình nón là: s = k²S = k²πl²cos2α