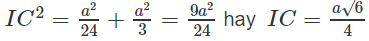Hình tứ diện đều ABCD có cạnh bằng a và có đường cao AH. Gọi O là trung điểm của AH

Bài 2: Mặt cầu

Bài 2.20 trang 61 Sách bài tập Hình học 12: Hình tứ diện đều ABCD có cạnh bằng a và có đường cao AH. Gọi O là trung điểm của AH. Xác định tâm và bán kính của mặt cầu ngoại tiếp tứ diện OBCD.

Lời giải:

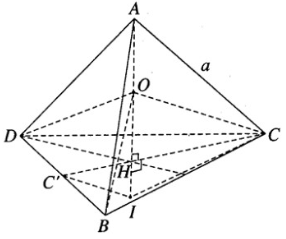
Gọi H trọng tâm của tam giác đều BCD.

Ta có AH ⊥ (BCD). Do đó

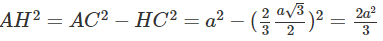
Vậy

Mặt khác OC² = OH² + HC²

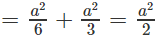
hay OC = OB = OD = (a√2)/2

Vì BD = BC = CD = a nên các tam giác DOB, BOC, COD là những tam giác vuông cân tại O. Do đó hình chóp ODBC là hình chóp có đáy là tam giác đều nên tâm của mặt cầu ngoại tiếp phải nằm trên OH, ngoài ra tâm của mặt cầu ngoại tiếp này phải nằm trên trục của tam giác vuông DOB. Từ trung điểm C’ của cạnh BD ta vẽ đường thẳng song song với OC cắt đường thẳng OH tại I. Ta có I là tâm mặt cầu ngoại tiếp tứ diện OBCD. Mặt cầu này có bán kính là IC và IC² = IH² + HC².

Chú ý rằng IH = OH/2 (vì HC′ = HC/2)

Do đó: