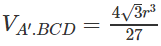Cho hình cầu đường kính AA’ = 2r. Gọi H là một điểm trên đoạn AA’ sao cho AH = 4r/3

Bài 2: Mặt cầu

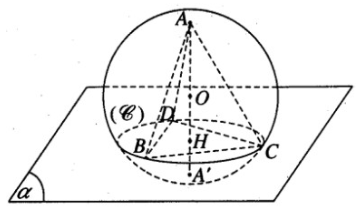
Bài 2.23 trang 61 Sách bài tập Hình học 12: Cho hình cầu đường kính AA’ = 2r. Gọi H là một điểm trên đoạn AA’ sao cho AH = 4r/3. Mặt phẳng (α) qua H và vuông góc với AA’ cắt hình cầu theo đường tròn (C).

a) Tính diện tích của hình tròn (C) .

b) Gọi BCD là tam giác đều nội tiếp trong (C), hãy tính thể tích hình chóp A.BCD và hình chóp A’.BCD.

Lời giải:

a) Theo giả thiết ta có AH = 4r/3

Ta suy ra OH = r/3. Gọi r’ là bán kính của đường tròn (C).

Ta có:

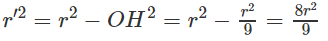
Vậy diện tích của hình tròn (C) là:

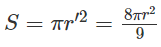
b) Vì BCD là tam giác đều nên ta có:

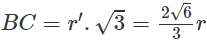
Diện tích của tam giác đều BCD là:

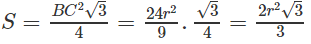
Thể tích hình chóp A.BCD là:

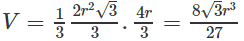
Hai hình chóp A.BCD và A’.BCD có chung mặt đáy BCD nên:

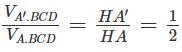
Do đó