Chứng minh rằng: i + i^2 + i^3 + ... + i^99 + i^100 = 0

Ôn tập cuối năm

Bài 21 trang 219 Sách bài tập Giải tích 12: Chứng minh rằng:

a) i + i² + i³ + ... + i⁹⁹ + i¹⁰⁰ = 0

b)

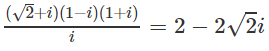
Lời giải:

a) Biến đổi vế trái bằng cách nhóm từng bốn số hạng và đặt thừa số chung, ta được

i(1 + i + i² + i³) + ... + i⁹⁷ (1 + i + i² + i³)

= (1 + i + i² + i³)(i + ... + i⁹⁷) = 0

Vì 1 + i + i² + i³ = 1 + i – 1 – i = 0

b) Ta có

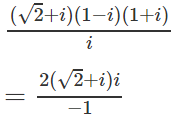
= −(2√2i + 2i²) = 2 − 2√2i